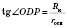Описанная пирамида
Если вершина пирамиды проектируется в центр окружности, которое является вписанным в основание пирамиды, то центр вписанного шара - точка пересечения высоты пирамиды с биссектрисой линейного угла двугранного угла при ребре основания.
В любую правильную пирамиду можно вписать шар, центр которого лежит на высоте пирамиды.
Точки соприкосновения шара и боковых граней лежат на высотах боковых граней, а точка касания вписанного шара и основания является центром окружности, вписанной в основание.
Во время решения задач на шар, вписанный в пирамиду, целесообразно рассмотреть определенные треугольники. На рисунке, приведенном ниже, такими треугольниками есть

;
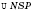
;
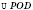
.
O - центр окружности, которое вписано в основание;
P - центр вписанного в пирамиду шара;
SO - высота пирамиды;
SD - высота боковой грани.
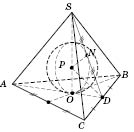
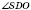
- линейный угол двугранного угла между плоскостью боковой грани
CSB и плоскостью основания;
DP - биссектриса
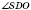
;
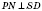
;
N - точка касания шара и боковой грани;
O - точка касания шара и основания;
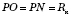
- радиус шара;
OD - радиус круга, вписанного в основание, -
rосн.
1. Рассмотрим

.
По свойству биссектрисы треугольника
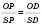
или
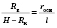
, где
l - длина апофеми.
2.
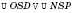
;
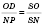
или
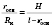 .
.
3. Рассмотрим
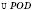 .
.