Тема 9. Корреляционные исследования в психологии

Под корреляцией (от лат. соггеШіо - “соотношение”) понимают реально установленный факт взаимосвязи определенного состояния одной переменной с определенными значениями другой, когда изменение одного из них сопровождается изменением второй. Иначе говоря, корреляция отражает факт ковариации переменных.

Корреляцию переменных х и у можно представить на так называемой диаграмме рассеивания или кореляційному поле (рис. 4).

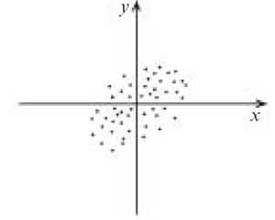
Рис. 4. Диаграмма рассеяния (корреляционное поле) результатов измерения переменных х и у

Множество точек (результатов измерения х и в) образует “облако”, по форме которой и судят о связи х и у. Чем больше есть такая связь, тем более вытянутой будет “тучка”.

Виды корреляций различают, во-первых, с особенностями сбора данных. При этом выделяют:

• аутохонні корреляции, которые представляют собой корреляцию результатов измерения одной и той же переменной на одних и тех же объектах - исследуемых в разное время, что дает возможность установить паттерн реакций и, следовательно, открывает путь к исследованию структуры личности;

• синхронные корреляции, которые устанавливают корреляции между различными переменными, были измерены одновременно (на одном и том же этапе исследования);

• перекрестно-отсроченную корреляцию между двумя переменными, которые измеряются в разный промежуток времени, например, одна - на первом этапе исследования, вторая - на конечном этапе [5; 9].

Во-вторых, корреляции различают по типом связи, при этом выделяют:

• линейную корреляцию, в которой выделяют позитивную, когда повышение уровня одной переменной сопровождается повышением другой, и отрицательную, когда рост уровня одной переменной сопровождается уменьшением уровня другой;

• нулевую, когда связь между переменными отсутствует;

• нелинейную корреляцию, когда повышение уровня одной переменной сопровождается ростом другого к определенным значений, а затем сопровождается ее уменьшением (рис. 5).

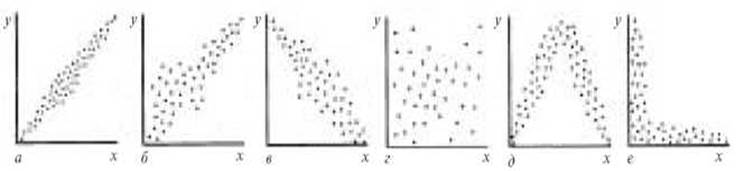
Рис. 5. Виды корреляций

(а и б - сильная и слабая положительные, в - отрицательная, г - нулевая, д и е - нелинейные корреляции) [4]

Примером нелинейной корреляции может быть известный закон Йеркса - Додсона, согласно которому в определенных показателей рост мотивации способствует повышению эффективности обучения, а потом эффект супермотивації снижает данную эффективность [3].

Статистической мерой корреляционной связи является прежде всего выборочный коэффициент ковариации переменных х и у:

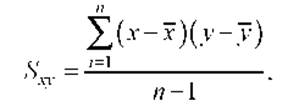
то есть среднее произведение отклонений каждой переменной.

Следует заметить, что ковариация переменной с самой собой является переменной дисперсией:

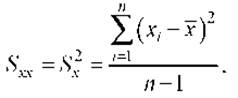
Чаще как статистическую меру связи между данными используют коэффициент корреляции, который представляет собой отношение полученной ковариации до максимально возможной:

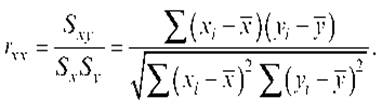
Значение коэффициента г (который называют коэффициентом Пирсона) тем больше, чем больше связь между переменными. При этом значимость этой связи зависит от принятого уровня значимости и величины выборки. Кроме коэффициента Пирсона, для данных, полученных по шкале интервалов можно использовать коэффициент ранговой корреляции Спирмена г:

где n - количество измерений переменных.

Для шкалы порядка с целью измерения связей между переменными используют коэффициент Кендалла, который основывается на подсчета разногласий в порядке ранжирования переменных х и у.

Для дихотомічної шкалы, которую иногда отождествляют со шкалой наименований, используют так называемый φ-коэффициент.

Например, результаты исследования групп мужчин и женщин, которые проходили определенное исследование и достигли (или не достигли) успеха, можно представить следующим образом (табл. 15):

Таблица 15

Представление результатов исследования по шкале дихотомічною

Тогда коэффициент ф можно определить по формуле

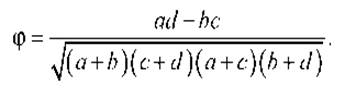
Отметим, что если переменная представлена множеством n-случаев со средним М и стандартным отклонением σ, ее значение можно преобразовать в другое множество данных со стандартным отклонением, которое равно 1. Тогда новые значения переменных будут непосредственно выражаться в отклонениях исходных значений от среднего, измеренных в единицах стандартного отклонения. Это особенно важно при необходимости сравнения результатов измерения переменных различной размерности. Для этого “сырые” баллы переводятся в стандартные оценки z по формуле

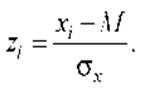
В этом случае коэффициент корреляции будет определяться по формуле

Следует заметить, что стандартную оценку для переменной можно получить, если стандартную оценку переменной х умножить на коэффициент корреляции между х и у:

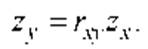
В результате на диаграмме рассеяния можно построить так называемую линию предсказания, которая сочетает средние оценки исследуемой переменной и тем самым позволяет предвидеть ее значение по оценкам переменной х (рис. 6)

Как видно из рис. 6, линия предсказания проходит через пересечение точек z_x = 0, z_y = 0, которые являются средними значениями соответствующих распределений.

Угол наклона линии предсказания определяется величиной коэффициента корреляции. При этом значению коэффициента корреляции, равный 0, соответствует горизонтальная линия, а значению коэффициента корреляции, равный 1, соответствует линия предсказания под углом наклона 45°.

Следует заметить, что предполагаемая величина (z_в) ближе к средней распределения, чем и величина, на основе которой делается предсказание (z_х), поэтому говорят, что предсказания направляются (регрессируют) до среднего, а линия предсказания также называется линией регрессии х на у.

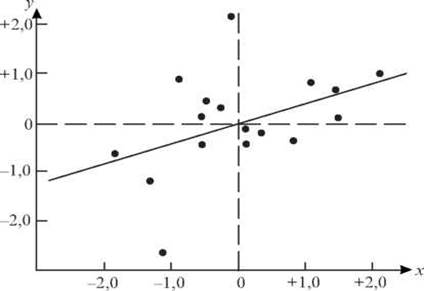
Рис. 6. Линия предсказания значений переменной по значениям переменной х

(по Г. Готтсданкером) [3]

Чем выше значение коэффициента корреляции, тем ниже регрессия предсказания. В случае полной корреляции регрессия к средней отсутствует, тогда, например, если значение z_х = 1,5, то и значение z_в = 1,5 и так для каждой пары значений переменных х и у.

Если корреляция между переменными отсутствует, то линия предсказания будет горизонтальной, и все предполагаемые значение в этом случае регрессируют до среднего.

Рассмотрена z-шкала является примером линейного преобразования значений переменной, при которой сохраняется соотношение между первичными и z-показателями, следовательно, сохраняются все свойства первичного распределения [1; 3].

Вышеуказанные рассуждения касаются тех случаев, когда форма распределения переменных х и в подобная. Если необходимо сравнить данные, представленные распределениями различной формы, используют нелинейные преобразования. А. Анастази отмечает о необходимости для такого рода вычислений перевести сначала “сырые” значения в процентили, а затем в нормализованные стандартные показатели [1].

Поиск и анализ указанных статистических мир связи используется, во-первых, как прием статистического анализа данных, когда, например, оценивается надежность экспериментальных результатов, валидность тестовых методик, или когда отсутствие корреляции позволяет отбросить гипотезу о причинно-следственной связи между переменными. Невозможность отклонения 0-гипотезы в последнем случае обусловлена отсутствием независимой и ковариации зависимой переменных, которая является существенным условием каузального вывода. Следовательно, коэффициент корреляции как мера

связи, может выполнять ту же роль, что и степени отличий (например, t-Стьюдента, дисперсионный анализ т.п.).

Во-вторых, оценка статистической меры связи является необходимой составляющей корреляционного исследования как средства эмпирической проверки психологических гипотез о естественные связи между переменными, уровни которых активно не изменяются, а только измеряются исследователем.

Итак, корреляционным исследованием, как правило, называют пассивно наблюдаемое исследования, которое имеет целью выявление статистической взаимосвязи между переменными и психологический прогноз на основе определенных інтеркореляцій [9].

Такого рода исследования широко используются в случае осложнения предмета, когда организация активных экспериментальных действий невозможна, затруднена или нежелательна, поскольку процессы, исследуются, могут потерять качественную специфику, если их искусственно изолировать. Например, довольно трудно, а из этических соображений и невозможно, исследовать каузальні связи между разводом родителей и развитием определенных личностных характеристик детей или, скажем, между порядком рождаемости и интеллектом. Здесь возможно установить только статистические связи.

Кроме того, корреляционное исследование, в отличие от эксперимента, позволяет в большинстве случаев быстро провести исследования, сэкономить деньги и время.

Следует заметить, что в случае установления значимой связи между переменными остается возможной большая количество объяснений (или теоретических гипотез) относительно характера и природы такой связи.

В частности, зависимость, возможно, есть каузальною, но направление связи может быть любым, при этом без экспериментального контроля невозможно отдать предпочтение ни одному из них.

Так, например, исследования взаимосвязи агрессивности и просмотра телевизионных передач не дают окончательного ответа относительно того, агрессивность побуждает к просмотру телевизионных передач определенной направленности, или, наоборот, такие передачи порождают агрессивное поведение [7].

Может оказаться, что переменные не будут связанные каузальным связью, но входят в комплекс взаимодействия, что другие каузальні зависимости порождают корреляцию между ними. Например, высокий уровень развития интеллекта может порождать корреляцию между успешностью обучения с математики и истории и является в этом случае скрытой переменной.

В связи с этим целесообразно осуществить проверку альтернативных объяснений относительно влияния “третьего скрытого фактора” путем статистического изъятия “подозреваемых” факторов влияния.

Например, Л. Ірон и Г. Х'юсманн обнаружили, что интенсивность просмотра фильмов со сценами насилия в 875 восьмилетних детей коррелировала с агрессивностью даже после статистического изъятие наиболее очевидных третьих факторов (численности семьи, статуса, образования родителей и т.д.). Более того, когда они снова исследовали этих самых детей в 19-летнем возрасте, оказалось, что просмотр жестоких боевиков в умеренной степени определяет агрессивность в 19 лет, но агрессивность в 8 лет не определяет увлечения жестокими боевиками в 19 лет. Это может означать, что не агрессивная склонность предопределяет стремление смотреть “крутые” фильмы, а скорее всего, “крутые” фильмы способны провоцировать человека на насилие, задавая определенные модели поведения [7].

Иногда корреляция может быть обусловлена неоднородностью выборки. Например, когда в выборку были отобраны мужчины - математики, а женщины - журналисты, можно установить корреляцию между полом и екстравертованістю.

Может также случиться, что корреляция между переменными обусловлена случаем и не имеет за собой опосредованного влияния скрытых переменных или других причин.

Итак, в исследовании кореляційному из-за отсутствия запланированного воздействия на зависимую переменную используются те характеристики, которые уже существуют, и это не дает возможности, как правило, установить причинно-следственные зависимости между переменными.

В то же время в отдельных случаях и в корреляционных исследованиях является возможным приблизиться к пониманию отношений между переменными как причинно-следственных подобно тому, как гіпотетико-дедуктивный метод рассуждений является характерным для собственно экспериментальных исследований и заключается в выводе из системы теоретических положений таких последствий-гипотез, которые могут быть проверены эмпирически с использованием процедур экспериментального контроля. Речь идет о возможности сравнения эмпирически выявленных корреляций с теми, что теоретически допускают в формальных каузальных моделях связей между переменными, как, например, в психогенетиці.

Планы корреляционных исследований часто рассматривают как формы контроля при получении эмпирических данных, то есть как аналог форм экспериментального контроля. Такие планы содержат:

• план измерения основных переменных;

• формы контроля диапазона их проявлений;

• формы контроля побочных переменных, которые обусловливают смешивание переменных.

Контроль побочных переменных в кореляційному исследовании осуществляется через составление однородных групп, которые выровненные по всем параметрам, кроме одного, что интересует исследователя.

Например, в известном исследовании влияния порядка рождаемости на интеллект различия, скажем, между 2 и 5 ребенком сравнивались в пределах однородных групп - семей, которые имели 5, 6, 7 и больше детей. Это позволило избежать смешения исследуемых переменных с побочным переменной - социально-экономическим положением семьи, поскольку семьи с низким социально-экономическим статусом, имеют, как правило, больше детей и худшие условия жизни, которые в целом могут негативно сказаться на уровне развития детей. И действительно, в этом исследовании было показано, что если исследуются группы с разной количеством детей в семьях, оказывается корреляционная связь между снижением показателей интеллекта и увеличением численности семьи [3; 6].

Следовательно, составление однородных групп представляет собой форму контроля в виде стабилизации всех уровней побочной переменной таким образом, чтобы на каждом уровне независимой переменной они были представлены равномерно. При этом количество однородных подгрупп равно количеству уровней побочных переменных.

Например, в указанном исследовании была выделена подгруппа с семьей из пяти детей и уже в середине этой группы изучалось влияние порядка рождения на интеллект [3].

Контроль побочных переменных с небольшим количеством исследуемых может также осуществляться путем подбора пар исследуемых, которые выровнены по побочной переменной, когда каждому индивиду одной группы подбирается индивид второй группы с такими же побочными характеристиками. При этом возникает угроза нерепрезентативності выборки, поскольку чем больше побочных переменных, тем меньше можно подобрать исследуемых с их равными значениями.

В целом контроль в корреляционных исследованиях является статистическим, что означает, во-первых, более-менее полный охват в выборке всех уровней случайных вариаций побочных переменных, во-вторых, рассмотрение эмпирически полученного коэффициента корреляции между переменными как мера оценки 0-гипотезы (об отсутствии связи между двумя или более показателями выборки).

В то же время в отличие от квазіекспериментальних схем “где и на ком проводить исследования”, в которых устанавливается причинно-следственная связь между переменными на основе контроля post factum (см. тему 8), в корреляционных исследованиях такой контроль, как правило, отсутствует [5].

Список использованной и рекомендуемой литературы

1. Анастази А., Урбина С. Психологическое тестирование. - СПб.: Питер, 2001. - С. 65-83, 104-109.

2. Головина Г. М., Крылов В. Ю., Савченко Г. Н. Математические методы в современной психологии: статус, разработка, применение. - М.: ИПРАН, 1995.

3. Готтсданкер Р. Основы психологического эксперимента: Пер. с англ. - М.: Изд-во МГУ, 1982. - С. 378-424.

4. Дружинин В. Н. Экспериментальная психология. - СПб.: Питер, 2000. - С. 140-168.

5. Кэмпбелл Д. Модели экспериментов в социальной психологии и прикладных исследованиях. - СПб.: Соц.-психол. центр, 1996. - 392 с.

6. Корнилова Т. В. Введение в психологический эксперимент. - 2-е изд. - М.: Изд-во МГУ; Изд-во ЧеРо, 2001. - С. 198-229.

7. Практикум по общей, экспериментальной и прикладной психологии /

В. Д. Балин, В. К. Гайда, В. К. Гербачевский и др.; Под общ. ред. А. А. Крылова, С. А. Маничева. - СПб.: Питер, 2000. - С. 5-32.

8. Психологическая диагностика / Под ред. К. М. Гуревича, Е. М. Борисовой. - М.: Изд-во УРАО, 2001. - С. 232-280.

9. Фресс П. Экспериментальный метод // Экспериментальная психология / Под ред. П. Фрессена, Же. Пиаже. - М.: Прогресс, 1966. - С. 148-155.

10. Шошин П. Б. Психологическое измерение. - М.: Изд-во МГУ, 1989. - Ч. 1. - 56 с.