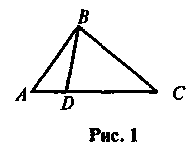Урок № 1
Тема. Четырехугольники
Цель: сформировать представление о четырехугольник, его элементы: вершина, сторона, диагональ, соседние стороны (вершины), противоположные стороны (вершины); ввести понятие периметра четырехугольника. Сформировать первичные умения:
· воспроизводить определение четырехугольника, его элементов;
· находить на рисунке изображение четырехугольника и его элементов;
· выполнять рисунки по описанию;
· решать простейшие задачи на вычисление с использованием понятия периметра четырехугольника.
Тип урока: усвоение новых знаний.
Наглядность и оборудование: конспект «Четырехугольники».
Ход урока
I. Организационный этап
Вступительное слово учителя о:
· особенности изучения геометрии в 8 классе;
· организацию учебного процесса в 8 классе;
· строение учебника.
II. Проверка домашнего задания
Учитель проверяет летнее домашнее задание (если такое было задано).
III. Формулировка цели и задач урока
Осознанному восприятию учащимися материала урока может способствовать работа с повторения и осознание важнейших понятий, изученных в 7 классе (эту работу проводим на этапе актуализации знаний и умений учащихся), в частности формируется мнение о том, что среди важнейших понятий курса геометрии 7 класса можно выделить треугольник. Необходимо обратить внимание учащихся на систему изучения геометрической фигуры «треугольник»: определение → элементы → свойства → понятие равенства → признаки равенства → решение задач с использованием теоретических сведений о треугольнике.
После проведенной работы с повторения определения и основных свойств треугольника предлагаем учащимся выполнить задание.
На плоскости даны 4 точки; рассмотрите все возможные случаи их взаимного расположения. Какие фигуры образуются, если совместить все возможные случаи их взаимного расположения? Возможные варианты взаимного расположения 4-х точек и фигур, образующихся в результате последовательного соединения точек отрезками.
Концентрируем внимание учащихся на случае, когда никакие три точки не лежат на одной прямой и никакие два отрезка не имеют общих внутренних точек, и таким образом формулируем основную дидактическую цель урока - изучить упомянутый случай и его простейшие свойства.
IV. Актуализация опорных знаний
Выполнение устных упражнений
1. Верны ли приведенные утверждения?
1) Через точку плоскости можно провести не менее 1000 прямых;
2) соединив попарно три точки на плоскости, всегда получим три прямые;
3) на каждой прямой можно выбрать по крайней мере 100 точек.
2. Сколько треугольников изображено на рисунке 1? Назовите их.
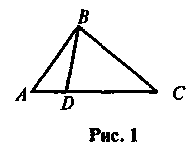
3. Сколько треугольников изображено на рисунке 2? Назовите их.
4. Найдите все треугольники (рис. 3), две вершины которых находятся в точках А и В.
5. Найдите все треугольники (рис. 4), две вершины которых находятся в точках А и В.
V. Усвоение знаний
План изучения нового материала
1. Определение четырехугольника.
2. Элементы четырехугольника.
3. Периметр четырехугольника.
@ Определение четырехугольника является одним из важнейших определений курса геометрии 8 класса. Именно поэтому осознанному восприятию этого определения поможет работа, проведенная на этапе формулировки цели урока: учащиеся должны понять, что для существования четырехугольника с вершинами в данных четырех точках необходимо одновременное выполнение двух условий:
· никакие три из данных четырех точек не должны лежать на одной прямой;
· никакие две стороны (отрезки, соединяющие эти точки) не должны иметь точек пересечения (внутренних).
Задачи. Есть четырехугольником фигура, образованная точками А, В, С и D и отрезками АВ, ВС, CD и AD?
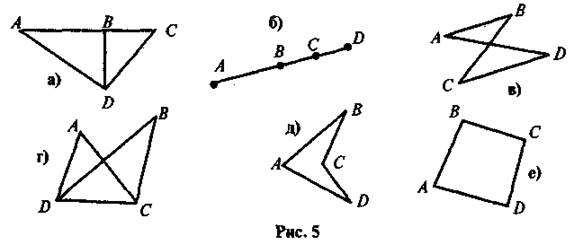
Во время изучения вопроса о элементы четырехугольника полезно было бы сделать сравнение с элементами треугольника (исследовать, как влияет увеличение количества вершин многоугольника на его элементы). Тогда понятно, что, в отличие от сторон и углов треугольника, стороны и углы четырехугольника могут быть по-разному расположены друг относительно друга (таким образом, вводится понятие противоположных, соседних, смежных сторон или вершин четырехугольника). Также важным является вопрос о правильном обозначение четырехугольника (в этом вопросе ученики часто допускают ошибки): важно, чтобы учеников осознали, что, в отличие от обозначения треугольника (все вершины которого называют в произвольном порядке), обозначая четырехугольник, вершины надо называть только последовательно (буквы, стоящие рядом в обозначении четырехугольника, определяют соседние вершины или одну из сторон четырехугольника). Осознанному восприятию этого фрагмента материала поможет работа с готовыми рисунками.
Задачи. Можно четырехугольники, которые изображены на рисунке 6, обозначить MNKP?
Сравнивая треугольник и четырехугольник, можно сформировать понятие диагонали четырехугольника (для осознания учащимися содержания этого понятия можно предложить вопрос о невозможности существования диагонали треугольника) и периметра четырехугольника.
Во время усвоения новых знаний целесообразно составлять с помощью учащихся опорный конспект, в котором теоретические сведения представлены в сжатом виде.
Конспект 1 |
Четырехугольники |
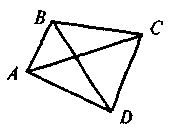
1. ABCD - четырехугольник.
Элементы четырехугольника:
а) точки А, В, С и D - вершины, причем А и В - соседние; А и С - противоположные;
б) отрезки АВ, ВС, CD и AD - стороны, причем: АВ и AD - соседние, АВ и CD - противоположные;
в) отрезки АС и BD - диагонали. |
|
2. Для четырехугольника ABCD сумма АВ + BC + CD+ AD - периметр;
P = AB + BC + CD + BD |
3.
|
ABCD - выпуклый четырехугольник; MNPQ - неопуклий четырехугольник. |
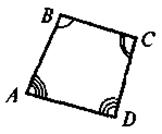
4. Если ABCD - выпуклый четырехугольник, то:  ABC ( ABC ( B); B);  BCD ( BCD ( C), C),  CDA ( CDA ( D) и D) и  DAB ( DAB ( A) - внутренние углы четырехугольника ABCD, причем A) - внутренние углы четырехугольника ABCD, причем  A + A +  B + B +  C + C +  D = 360° D = 360° |
|
|
|
|
VI. Формирование первичных умений
Выполнение устных упражнений
1. Сколько соседних вершин имеет вершина четырехугольника? Сколько противоположных? Назовите соседние и противоположные вершины для вершины В четырехугольника ABCD.
2. Сколько соседних сторон сторона четырехугольника? Сколько противоположных? Назовите соседние и противоположные стороны для стороны AD четырехугольника ABCD.
3. Отрезок, который соединяет две вершины четырехугольника, не является его диагональю. Могут ли данные вершины быть противоположными?
4. Вершинами четырехугольника являются точки К, L, М, N.
а) Известно, что KM и ML - стороны четырехугольника. Назовите его диагонали.
б) Известно, что KL - диагональ четырехугольника. Назовите вершины, соседние с вершиной К.
в) Данный четырехугольник можно назвать KMLN. Можно ли его назвать MLAN?
Выполнение графических упражнений
Отметьте точки А, В, С и D, не лежащих на одной прямой, и последовательно совместите их отрезками так, чтобы образовался четырехугольник. Дайте название полученному четырехугольнике и проведите его диагонали.
Выполнение письменных упражнений
1. Найдите периметр четырехугольника, если его наименьшая сторона равна 5 см, а каждая следующая сторона на 2 см больше предыдущей.
2. Найдите стороны четырехугольника, если его периметр равен 3 дм, а одна сторона меньше каждой из трех других на 2 см, 3 см и 5 см соответственно.
3*. Периметр четырехугольника ABCD равен 23 дм. Найдите длину диагонали АС, если периметр треугольника ABC равен 15 дм, а периметр треугольника ADC равен 22 дм.
VII. Итоги урока
Тестовое задание
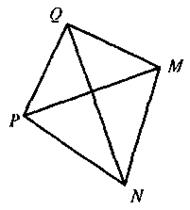
Какое из утверждений неверное? В четырехугольнике PQMN (см. рис):
1) вершины М и N, соседние с вершиной Q;
2) вершина N противоположная вершине Q;
3) отрезки QN и РМ - диагонали;
4) NP и NM - соседние стороны.
VIII. Домашнее задание
Изучить содержание основных понятий урока. Решить задачи.
1. Существует ли четырехугольник ABCD, в котором АВ = 9 см, ВС = 12 см, АС = 21 см? Ответ обоснуйте.
2. Периметр четырехугольника равен 20 см. Найдите стороны четырехугольника, если один из них составляет 40 % периметра, а три другие уровни.
3. Стороны четырехугольника относятся как 3 : 4 : 5 : 6. Найдите периметр четырехугольника, если сумма его наибольшей и наименьшей сторон равна 18 см.
4. (На повторение). Известно, что AKMN=ANPK (см. рис).
а) Докажите, что MK || NP;
б) найдите  P, если
P, если  M = 65°.
M = 65°.