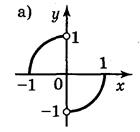|
Зависимость у·= f(x) является функцией, х - независимая переменная, у - зависимая переменная. f(9) = 39, f(12) = 38.5,..., f(24) = 37. D(f) = {9;12;15; 18; 21; 24}. E(f) = {39; 38,5; 38,3; 37,3; 37,1; 37}. Функцию можно задать с помощью таблицы, графика, формулы. Чаще всего функцию задают формулой, которая дает возможность получить значение зависимой переменной у, подставив предельное значение аргумента х. Например. Если каждому значению х из множества действительных чисел поставить в соответствие квадрат этого числа, то-функцию можно записать в виде формулы: у = х2 или f(x)= x2. Областью определения функции у = f(x), которая задана формулой, называется множество тех значений, которые может принимать х, то есть формула имеет смысл (все действия, указанные формуле, можно выполнить). При нахождении области определения следует помнить: 1) Если функция является многочленом в = аn хn + αn-1 xn-1 +... + α1x + a0, то D(y) = (- 2) Если функция имеет вид у = 3) Если функция имеет вид у = Графиком функции у = f(x) называется множество всех точек плоскости с координатами (x;f(x)) , где первая координата «пробегает» всю область определения функции у = f(x), а вторая координата - это соответствующие значения функции в точке х. Выполнение упражнений
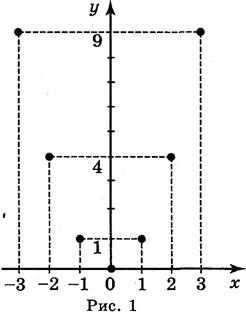
1. Найдите значение функции: a) f(x) = б) f(x) = Ответ: а) f(1) = 2, f(-1) = 0; f(5) = 1,2; б) f(3) = 0; f(12) = 3; f(52) = 7 2. Функция задана формулой у = x2 на области определения D = {-3; -2; -1; 0; 1; 2; 3}. Задайте ее с помощью: а) таблицы; б) графика. Ответ:
б) рис. 1
3. Найдите область определения функции: а) у = х2 + х3; б) Ответ: a) D(y) = R; б) D(y) = (- 4. Найдите область значений функции: а) у = Ответ: а) Е(у) = [2; +
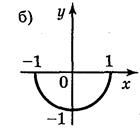
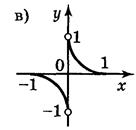
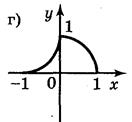
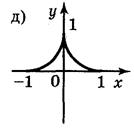
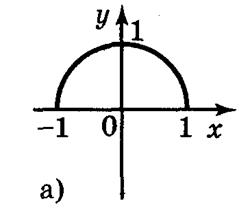
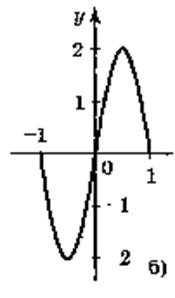
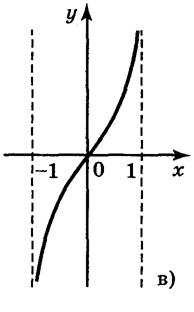
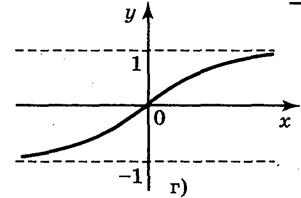
5. Для функций, графики которых изображены на рис. 2, укажите D(y) и Е(у).
Рис. 2
Ответ: а) D(у) = [-1;1]; Е(у) = [0;1]; б) D(y) = [-1;1]; E(y) = [-2;2]; в) D(y) = (-1;1); E(у) = R; г) D(y) = R; Е(у) = (-1;1). 6. Какие из линий, изображенных на рисунке 3, является графиком функции? Почему?
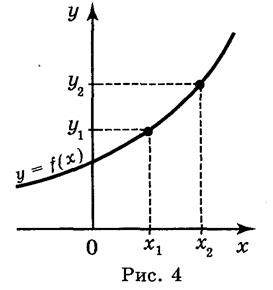
Ответ: а); в). III. Систематизация и обобщение знаний учащихся о убывающие, возрастающие, четные и нечетные функции. Функция у = f(x) называется возрастающей (рис. 4), если большему значению аргумента соответствует большее значение функции, т.е. для любых значений х1 и х2 из области определения функции таких, что х1 х2, выполняется неравенство f(x1) f(x2) и наоборот: из того, что f(x1) f(x2) выполняется неравенство х1 х2.
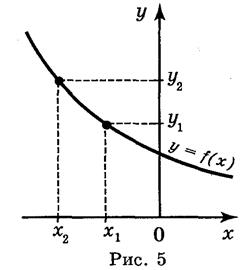
Функция у = f(x) называется убывающей (рис. 5), если большему значению аргумента соответствует меньшее значение функции, т.е. для любых значений х1 и х2 из области определения функции таких, что х1 х2, выполняется неравенство f(x1) > f(x2) и наоборот: если у = f(x) - убывающая, то из того, что f(x1) > f(x2), выполняется неравенство х1 х2.
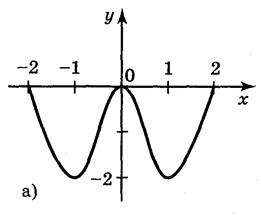
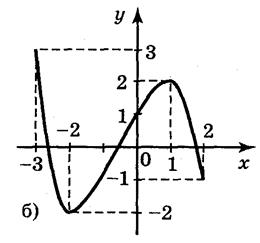
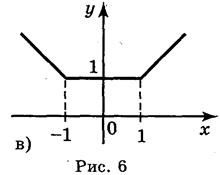
Выполнение упражнений 1. Пользуясь графиками функций, изображенных на рисунке 6, укажите промежутки возрастания и убывания функций.
Ответ: а) на каждом из промежутков[-1;0], [1;2] функция возрастает на каждом из промежутков[-2;-1], [0;1] функция спадает; б) на каждом из промежутков[-3;-2], [1;2] функция убывает; на промежутке [-2;1] функция возрастает; в) на промежутке (- 2. Функция у = f(x) возрастающая. Сравните: а) f(10) и f(-10); б) Ответ: а) f(10) > f(-10); б) 3. Функция у = f(x) - убывающая на R. Сравните: а) f(10) и f(-10); б) Ответ: а) f(10) f(-10); б) 4. Найдите промежутки возрастания и убывания функции: а) у = x - 3; б) у = -x + 3; в) у = x2 + 1; г) у = -х2 + 1. Ответ: а) возрастает на R; б) убывает на R; в) возрастает на промежутке [0;+ г) возрастает на промежутке (-
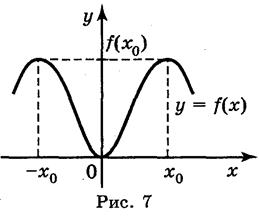
Функция у = f(x) называется парной, если для любого значения х из D(y) значение - х также принадлежит D(y) и выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ОУ (рис. 7).
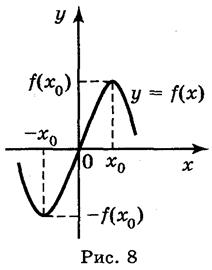
Пример 1. Или четная функция f(x) = χ4 + χ2 ? Поскольку D(f) = R и f(-x) = (-х)4 + (-x)2 = х4 + х2 = f(x) , то функция четная. Пример 2. Или четная функция f(x) = х2 + х ? Поскольку D(f) = R, но f(-x) = (-х)2 + (-х) = х2 - х Функция у = f(x) называется нечетной, если для любого значения х из D(y) значение х График нечетной функции симметричен относительно начала координат (рис. 8).
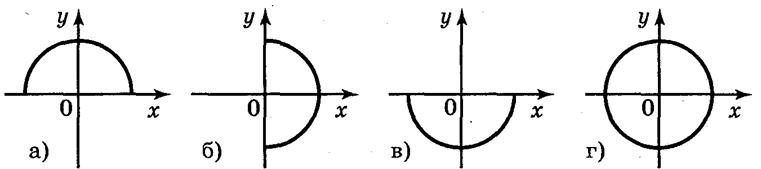
Пример 3. Или нечетная функция f(х) = x3 - x5? Поскольку D(f) = R и f(-х) = (-х)3 - (-х) = -х3 + х5 = -(х3 - х5) = -f(х), то функция нечетная. Пример 4. Или нечетная функция f(х) = х3 - х2 ? Поскольку D(f) = R и f(-x) = (-х)3 - (-х)2 = -х3 - х2 = -(х3 + х2) Выполнение упражнений1. Какие из функций, графики которых показаны на рисунке 9, являются четными, а какие нечетными?
Рис. 9
Ответ: нечетные - а), в); парные - б) д). 2. Какие из представленных функций а) у = х3 + 2х7; б) у = Ответ: четные - в), г); е); нечетные - а).
IV. Подведение итогов урока
V. Домашнее задание Раздел И § 1(1). Вопросы и задания для повторения раздела И № 1-12. Упражнения№ 1 (2; 5; 7), № 2 (3; 5).
|
|
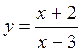 ; в)
; в) 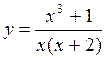 ; д)
; д) 
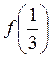 и
и 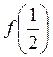 .
.