Прикладные задачи

Прогрессии имеют прикладное значение.

Так, например, из физики известно, что любое тело при свободном падении за каждую следующую секунду проходит на 9,8 м больше, чем за предыдущую, то есть отрезки пути, который проходит тело за каждую секунду, образуют арифметическую прогрессию.

Из биологии известно, что при нормальных условиях бактерии размножаются так, что их количество увеличивается вдвое каждые 30 минут. Т.е. из одной бактерии за 3 часа будем иметь 64 бактерии. Количества бактерий образуют геометрическую прогрессию. Говорят, что бактерии размножаются в геометрической прогрессии.

Иногда приходится иметь дело с бесконечными десятичными периодическими дробями, которые необходимо превращать в обычные дроби. При этом можем пользоваться такими правилами:

1. Если в бесконечной десятичной периодической дроби целая часть равна нулю, a период стоит сразу после запятой, то дробь равна обычной дроби, числитель которой содержит число, стоящее в периоде, a знаменатель содержит число, состоящее из такого количества цифр 9, сколько цифр в периоде. Например, дробь 0,(173) = .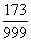

2. Если в бесконечной десятичной периодической дроби целая часть равна нулю, a перед периодом стоят десятичные знаки, то такая дробь равна обычной дроби, числитель которого содержит число, равное разности числа, образованного всеми цифрами от запятые до конца первого периода и числа, образованного цифрами, стоящими от комы до начала периода, a знаменатель содержит число, состоящее из такого количества цифры 9, сколько цифр в периоде, и столько нулей, сколько знаков от запятой до первого периода. Например, дробь 0, 21(13) = 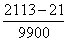, то есть .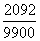