Сумма первых n членов геометрической прогрессии

Распространенной является задача на нахождение суммы первых n членов геометрической прогрессии. Для этого достаточно знать первый член прогрессии b₁ и знаменатель прогрессии q.

Формула суммы S_n n первых членов геометрической прогрессии .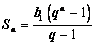

Если знаменатель геометрической прогрессии q = 1, то прогрессия является постоянной, все ее члены равны, поэтому сумма n первых ее членов равна произведению одного члена прогрессии на их количество.

Рассмотрим бесконечную геометрическую прогрессию, знаменатель которой удовлетворяет условию |q| 1. Члены такой прогрессии будут приближаться к нулю. Для этих прогрессий можно находить суммы всех членов по формуле .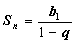

Старинная задача

В учебнике Магницкого «Арифметика» есть такая задача:

Некто продал лошадь за 156 рублей. Но покупатель вернул товар, считая, что цена великовата. Тогда продавец предложил ему купить только гвоздики до подков лошади. Гвоздей в каждой подкове 6, а цена была предложена такая: за первый гвоздь - четверть копейки, за второй - полушки, за третий - одну копейку и так далее. Покупатель решил, что при таких подсчетах он заплатит за коня не больше 10 рублей и согласился на условие. Подсчитав, сколько ему нужно заплатить за 24 подковы, то есть найти сумму 24 первых членов геометрической прогрессии, первый член которо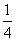й - копейки, a знаменатель прогрессии равен числу 2, мы поймем, насколько больше заплатил жадный покупатель - эта сумма равна почти 42 тысячам рублей.