Геометрическая прогрессия, ее свойства.

Формула n-го члена геометрической прогрессии

Некоторые результаты естественных процессов образуют последовательность называется геометрической прогрессией.

Геометрическая прогрессия - это последовательность, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же отличное от нуля число, которое называется знаменателем геометрической прогрессии. В геометрической прогрессии каждый член, начиная с второго, является срединно геометрическим между двумя соседними членами: .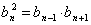

Знаменатель геометрической прогрессии ( b_n обозначается q и равна отношению любого члена прогрессии, начиная со второго, к предыдущему члену: 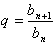. Вообще, если b_i и b_j - два данные члены геометрической прогрессии ( b_n, причем i j, то .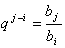

Любой член геометрической прогрессии можно вычислить, зная первый член прогрессии b₁ и знаменатель прогрессии q по формуле n-го члена геометрической прогрессии b_n = b₁q^n-1.

Свойства геометрической прогрессии с первым членом b₁ и знаменателем q:

1. Если первый член геометрической прогрессии - число положительное (b₁ > 0) и знаменатель прогрессии q > 1, то такая геометрическая прогрессия является возрастающей; или если первый член геометрической прогрессии - число отрицательное (b₁ 0) и знаменатель прогрессии 0 > q 1, то такая геометрическая прогрессия является возрастающей.

2. Если первый член геометрической прогрессии - число отрицательное (b₁ 0) и знаменатель прогрессии q > 1, то такая геометрическая прогрессия является убывающей; или если первый член геометрической прогрессии - число положительное (b₁ > 0) и знаменатель прогрессии 0 q 1, то такая прогрессия является убывающей; При q 0 геометрическая прогрессия не является ни убывающей, ни растущей.

3. Произведение двух членов конечной геометрической прогрессии, равноотстоящих от ее концов, равен произведению крайних членов.