Сумма первых n членов арифметической прогрессии

Часто рассматривают не всю прогрессию, a ее часть с первых n членов a₁, a₂, ..., a_n.

Сумма n первых членов конечной арифметической прогрессии равна полусумме ее крайних членов, умноженной на число членов. Формула суммы S_n n первых членов конечной арифметической прогрессии .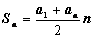

Рассмотрим задачу на нахождение суммы первых n членов натурального ряда.

Первые n членов натурального ряда образуют арифметическую прогрессию с первым членом, равный единице, последним членом, равна n, и разностью, равной единице. Сумма крайних членов прогрессии равен 1 + n, тогда сумма всех n членов равна .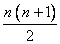

В случае, когда известны первый член прогрессии a₁ и ее разность d, для нахождения суммы S_n n первых членов конечной арифметической прогрессии используем формулу 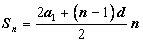.