Розв'язуванян неравенств второй степени с одной переменной графическим способом. Метод интервалов

Иногда для исследования функций необходимо решать неравенства второй степени с одной переменной, то есть квадратичные неравенства.

Квадратичная неравенство - это неравенство, в которой одной частью является ноль, a второй - выражение вида ax² + bx + c, где a, b, c - действительные числа, причем a ≠ 0.

Рассмотрим способ решения квадратичных неравенств с помощью графика функции. Он заключается в том, чтобы выяснить, для каких значений переменной х график функции, задаваемой тричленом ax² + bx + c, находится в верхний півплощині (то есть приобретает положительных значений), и при которых - в нижний півплощині (то есть приобретает отрицательных значений), и выбрать те значения, которые соответствуют заданной неровности.

Введем и определим функцию ƒ(x) = ax² + bx + c:

1. Если дискриминантов трехчлена отрицателен (D 0), то график функции не пересекает ось абсцисс, и

· при положительном первом коэффициенте a > 0 функция приобретает положительных значений (ƒ(x) > 0) для всех действительных значений переменной x(-∞,∞);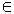

· при отрицательном первом коэффициенте a 0 функция приобретает отрицательных значений (ƒ(x) 0) для всех действительных значений переменной x (-∞,∞).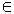

2. Если дискриминантов трехчлена равен нулю (D = 0) - график примыкает к оси абсцисс в точке x₁, и

· при a > 0 функция принимает положительные значения (ƒ(x) > 0) для всех действительных значений переменной, кроме значения x₁ (x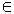 (-∞, x₁) U (x₁, ∞));

· при a 0 функция приобретает отрицательных значений (ƒ(x) 0) для всех действительных значений переменной, кроме значения x₁ (x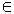 (-∞, x₁) U (x₁, ∞)), где x₁ - корень квадратного трехчлена ax² + bx + c.

Если заданное неравенство нестрогая, то значение x₁ не изымается.

3) Если дискриминантов трехчлена положительный (D > 0), то график пересекает ось абсцисс в точках x₁ и x₂, и

· при a > 0 функция приобретает положительных значений (ƒ(x) > 0) для всех действительных значений переменной, принадлежащих объединению промежутков x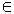 (-∞, x₁) U (x₂, ∞); функция приобретает отрицательные значения для всех значений переменной, принадлежащих промежутке (х₁; х₂);

· при a 0 функция приобретает отрицательных значений (ƒ(x) 0) для всех действительных значений переменной, принадлежащих объединению промежутков x (-∞, x₁) U (x₂, ∞); функция принимает положительные значения для всех значений переменной, которые принадлежат промежутку (х₁; х₂).