Соотношение между сторонами правильных многоугольников и радиусами вписанного и описанного кругов

Для правильных многоугольников существует понятие центрального угла многоугольника - угла между двумя отрезками, соединяющими центр многоугольника с двумя его соседними вершинами. Градусная мера центрального угла правильного многоугольника равна 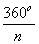. В правильном многоугольнике отрезок, соединяющий центр с вершиной многоугольника многоугольника, является радиусом круга, описанного вокруг этого многоугольника. Радиус описанной окружности равен отношению стороны многоугольника к удвоенного синуса половины центрального угла многоугольника. 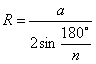, где а - это сторона многоугольника, а n - количество углов многоугольника.

В правильном многоугольнике отрезок, соединяющий центр многоугольника с серединой стороны многоугольника, является радиусом круга, вписанного в этот многоугольник. Радиус вписанной окружности равен отношению стороны многоугольника до удвоенного тангенса половины центрального угла многоугольника: 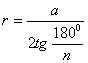, где а - это сторона многоугольника, а n - количество углов многоугольника.

Запомнить’помните!

В правильном треугольнике радиус описанной окружности равна стороне, деленной на корень квадратный 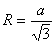из числа 3: , а радиус вписанного круга равен стороне треугольника, деленной на два корня квадратных из числа 3: 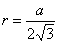. У правильного треугольника радиус описанной окружности вдвое больше радиуса вписанного круга.

В правильном четырехугольнике радиус описанного круга равна стороне, деленной на корень квадратный из числа 2: 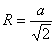, а радиус вписанной окружности равен половине стороны четырехугольника: r = a/2..

В правильному шестиугольнику радиус описанного круга равна стороне многоугольника 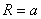, а радиус вписанной окружности равен половине стороны шестиугольника, умноженной на корень квадратный из числа 3: 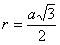.