Теорема синусов

Соотношение между сторонами и противоположными к ним углов любого треугольника выражается в теореме синусов:

Стороны треугольника пропорциональны синусам противоположных углов.

Если в треугольнике три стороны обозначить как a, b, c , и противоположные им углы соответственно α, β, γ, то справедливым является соотношение:

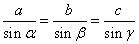. Если треугольник является вписанным в круг с радиусом R, то отношение сторон треугольника к синусу противоположных им углов равна двум радиусам описанной окружности (т. е. равна диаметра описанной вокруг треугольника окружности).

Из теоремы синусов следует, что в треугольнике против большей стороны лежит больший угол и наоборот, против большего угла лежит большая сторона.