Решение треугольников

Теорема косинусов

В любом треугольнике все три его стороны и угол между двумя из них имеют свойство, которое выражается в теореме косинусов:

Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.

Если в треугольнике три стороны обозначить как a, b, c, и противоположные им углы соответственно α, β, γ , то справедливы соотношения:

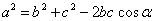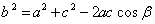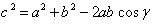. . . Из теоремы косинусов следует, что квадрат любой стороны треугольника равен сумме квадратов двух других сторон плюс минус удвоенное произведение одной из сторон в проекции второй стороны. Если противоположный угол острый, то берем знак минус, если противоположный угол тупой, берем знак плюс.

Если квадрат некоторого стороны треугольника меньше сумму квадратов двух других сторон, то противоположный ему угол является острым.

Если квадрат некоторого стороны треугольника больше суммы квадратов двух других сторон, то противоположный ему угол является тупым.

Если квадрат некоторого стороны треугольника равен сумме квадратов двух других сторон, то противоположный ему угол является прямым.

Из теоремы косинусов следует формула косинуса любого угла треугольника:

Косинус некоторого угла треугольника равен отношению суммы квадратов сторон, прилегающих к этому угла без квадрата противоположного ему стороны до удвоенного произведения прилегающих к углу сторон.

.

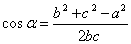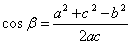
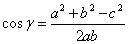. С помощью теоремы косинусов можно доказать теорему о диагонали параллелограмма:

Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов двух его смежных сторон.