Часть 3 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
Раздел 9 МАГНЕТИЗМ. МАГНИТНОЕ ПОЛЕ ЭЛЕКТРИЧЕСКОГО ТОКА
9.6. Движение заряженной частицы в магнитном и электрическом полях. Сила Лоренца
Проводник, по которому проходит ток,
отличается от проводника без тока тем, что в нем происходит
упорядоченное движение носителей зарядов. Это наводит на мысль о том, что сила, которая действует
на проводник с током, помещенная в магнитное поле, обусловлена действием сил на отдельные
движущиеся заряды. А уже от этих зарядов действие передается проводнику, по которому они
перемещаются. Такой подход дает возможность определить силу, которая действует на отдельный заряд,
что движется в магнитном поле. Ее называют силой Лоренца.
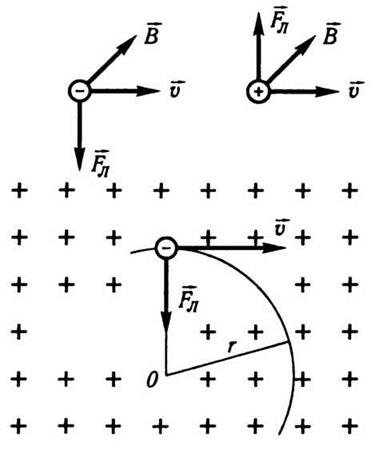
Рис. 9.7
Пусть электрон, имеющий скорость  , влетает в однородное
магнитное поле с индукцией
, влетает в однородное
магнитное поле с индукцией 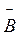 в, как показано на рис. 9.7. Линии
индукции магнитного поля помечены крестиком и направленные от читателя перпендикулярно
к плоскости рисунка. Движущаяся заряженная частица является электрическим микротоками. Тогда
для определения силы, с которой магнитное поле действует на движущийся заряд е (е - заряд
электрона), можно воспользоваться законом Ампера. По закону Ампера на элемент l прямолинейного тока однородное
магнитное поле с индукцией
в, как показано на рис. 9.7. Линии
индукции магнитного поля помечены крестиком и направленные от читателя перпендикулярно
к плоскости рисунка. Движущаяся заряженная частица является электрическим микротоками. Тогда
для определения силы, с которой магнитное поле действует на движущийся заряд е (е - заряд
электрона), можно воспользоваться законом Ампера. По закону Ампера на элемент l прямолинейного тока однородное
магнитное поле с индукцией 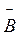 действует с силой, равной IlBsin α [формула (9.21)] (α - угол между направлениями поля и тока).
Пусть движущийся заряд е за время t переместится на расстояние l. Это подобно элемента тока,
сила которого И =
действует с силой, равной IlBsin α [формула (9.21)] (α - угол между направлениями поля и тока).
Пусть движущийся заряд е за время t переместится на расстояние l. Это подобно элемента тока,
сила которого И = 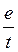 .
Подставив это выражение для И в формулу (9.21),
получим
.
Подставив это выражение для И в формулу (9.21),
получим 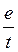 lBsin α. Учитывая, что в
этом случае sin α = l и l/t = υ, окончательно получим выражение для силы Лоренца:
lBsin α. Учитывая, что в
этом случае sin α = l и l/t = υ, окончательно получим выражение для силы Лоренца:

Для определения направления силы Лоренца
можно применить правило левой руки. Однако в этом случае пальцы нужно
разместить не в направлении движения электрона, а против движения его, поскольку электрон заряжен
негативно, а за направление тока взято направление движения положительных зарядов.
Воспользовавшись понятием о векторное произведение, формулу (9.26) можно представить в
таком виде:

Тогда соотношение (9.27) одновременно
со значением определять и направление силы, действующей в магнитном поле на движущийся
электрон. Направление силы, действующей в магнитном поле на положительно заряженную частицу,
совпадает с направлением векторного произведения [ ,
,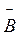 ], то есть
], то есть

Формулы (9.27) и (9.28) можно
объединить

но
под q следует понимать алгебраическое значение
заряда, что движется (q > 0 для положительных зарядов и q 0 для отрицательных). На рис. 9.7
показано взаимное расположение векторов 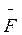 л,
л,  ,
,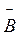 для положительного и отрицательного зарядов.
для положительного и отрицательного зарядов.
Поскольку сила Лоренца 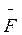 л всегда направлена перпендикулярно к скорости движения
заряженной частицы, то она не выполняет работы, а лишь изменяет направление движения
заряженной частицы в магнитном поле. Абсолютное значение скорости заряженной
частицы и кинетическая энергия при этом не меняются. Сила Лоренца является
центростремительной силой и предоставляет заряженной частице центростремительного ускорения,
равен
л всегда направлена перпендикулярно к скорости движения
заряженной частицы, то она не выполняет работы, а лишь изменяет направление движения
заряженной частицы в магнитном поле. Абсолютное значение скорости заряженной
частицы и кинетическая энергия при этом не меняются. Сила Лоренца является
центростремительной силой и предоставляет заряженной частице центростремительного ускорения,
равен 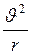 ,
где υ - скорость движения электрона; r -
радиус кривизны траектории электрона в магнитном поле. Тогда, учитывая
перпендикулярность векторов
,
где υ - скорость движения электрона; r -
радиус кривизны траектории электрона в магнитном поле. Тогда, учитывая
перпендикулярность векторов  i
i 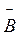 , запишем
, запишем
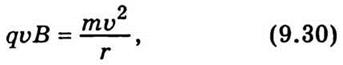
где
q - заряд частицы; m - ее масса.
Из формулы (9.30) видно, что траектория
заряженной частицы, которая влетает в однородное магнитное поле (в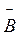 = const) под углом
= const) под углом 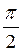 к линиям магнитной индукции, имеет
одинаковую кривизну, следовательно, является кругом, радиус которого, исходя из равенства (9.30),
равна
к линиям магнитной индукции, имеет
одинаковую кривизну, следовательно, является кругом, радиус которого, исходя из равенства (9.30),
равна

Если в пространстве, где движется
заряженная частица, создать магнитное поле, напрямлене под углом α к ее скорости, то дальнейшее движение
частицы можно рассматривать как геометрическую сумму двух движений, происходящих
одновременно, а именно: вращение по кругу со скоростью υsinα в плоскости, перпендикулярной к силовым линиям, и
перемещение вдоль поля со скоростью υcosα. Следовательно, траектория частицы в этом случае приобретает форму
винтовой линии, ось которой параллельна направлению вектора 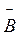 (рис. 9.8).
(рис. 9.8).
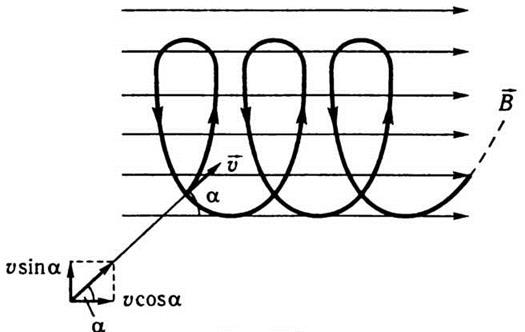
Рис. 9.8
Влияние электрического поля на движение
электрона или другой заряженной частицы существенно отличается от влияния
магнитного поля. Электрическое поле изменяет кинетическую энергию электрона, тогда как магнитное
поле изменяет только направление движения, а не его скорость. Движение заряженной частицы,
например электрона в электрическом поле в общем случае подобный движения
тела в гравитационном поле: если начальная скорость электрона противоположна
направления силовых линий однородного электрического поля, то сила, действующая на него,
совпадает с направлением скорости - электрон движется рівноприскорено. При
обратном направлении скорости он будет двигаться рівносповільнено. Если начальная
скорость электрона перпендикулярна к направлению силовых линий однородного
электрического поля, то электрон будет двигаться по параболе.
Сила, действующая со стороны однородного
электрического поля на электрон, который влетает в него перпендикулярно к линиям
напряженности, только в начальный момент является центростремительной. Следовательно, радиус кривизны r такого электрона для начальной
точки параболы можно вычислить из соотношения

где
Е - напряженность электрического поля; m
- масса электрона. Таким образом, для электронов, отклоняющихся поперечным
электрическим полем, радиус кривизны траектории пропорционален квадрату скорости:

В общем случае на подвижной
электрический заряд q может одновременно действовать магнитное поле
с индукцией 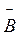 и
электрическое поле характеризуется напряженностью
и
электрическое поле характеризуется напряженностью 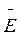 .
Тогда результирующая сила
.
Тогда результирующая сила 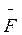 , действующая на заряд,
равна векторной сумме силы
, действующая на заряд,
равна векторной сумме силы 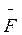 е = q
е = q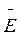 , которая действует на заряд со стороны электрического
поля, и силы Лоренца
, которая действует на заряд со стороны электрического
поля, и силы Лоренца 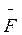 л = q[
л = q[ ,
,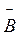 ]:
]:

Это выражение называют формулой
Лоренца. Согласно (9.31) при отклонении электрона магнитным полем радиус
кривизны его траектории пропорционален первой степени скорости. Эту особенность
используют для измерения скорости движения электронов методом взаимной
компенсации действия электрического и магнитного полей на движение электрона.
Если разместить плоские полюса
электромагнита так, чтобы магнитные силовые линии были перпендикулярны к силовым
линий электрического поля и поток электронов проходил одновременно между полюсами
электромагнита и пластинами плоского конденсатора, то, регулируя силу тока в
обмотке электромагнита (изменяя индукцию магнитного поля), отклонение
электронов от прямолинейного пути, вызванное электрическим полем, можно
полностью компенсировать одинаковым по значению, но противоположен по направлению
отклонением, вызванным магнитным полем. Из формул для радиусов кривизны
траектории электронов в поперечном электрическом (9.33) и магнитном (9.31)
полях видно, что отклонение можно взаимно компенсировать, если
выполняется
соотношение 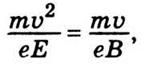 или
или

Эта формула дает возможность определить
скорость заряженных частиц (электронов) измерением напряженности
электрического и индукции магнитного полей, подобранных так, чтобы их распашные
действия взаимно компенсувались. Если после этого устранить электрическое поле и измерить
отклонение электронов в магнитном поле, то при r, Е и В можно определить удельный заряд электрона -
отношение заряда электрона к его массе. Формулу для вычисления этого
отношение можно получить из (9.31) и (9.35):

Удельный заряд электрона был впервые
определен Дж. Томсоном. На основе измерений отклонения катодных лучей в
электрическом и магнитном полях было установлено, что

Учитывая, что элементарный заряд е
= 1,602 ∙ 10-19 Кл, и зная е/m, получим, что масса электрона m = 9,109 ∙ 10-31 кг.
Рассмотрен метод определения е/т,
можно применять тогда, когда все частицы в потоке имеют одинаковую скорость.
Все электроны, образующие пучок, ускоряются одной и той же разницей
потенциалов, которую приложено между катодом, из которого они вылетают, и анодом; поэтому
разброс значений скоростей электронов в потоке очень мал.
Положительные ионы образуются за
счет ионизации молекул газа. Возникая в разных местах, ионы преодолевают
разную разность потенциалов, вследствие чего скорости различных ионов
отличаются друг от друга. Поэтому метод, с помощью которого было определено
удельный заряд электронов, нельзя применять к ионам.
В 1907 г. Дж. Томсон разработал «метод парабол», с помощью которого можно определить
удельный заряд ионов.
Проделав опыт с химически чистым
неоном, Дж. Томсон
выяснил, что этот газ
образовывал две параболы, соответствующие атомным массам 20 и 22. Попытки
объяснить этот результат привели к предположению о существовании двух химически
неделимых разновидностей атомов неона (по современной терминологии - два изотопа
неона). Доказал это предположение Ф. Астон, который усовершенствовал метод определения удельного
заряда ионов. Прибор, с помощью которого можно определить е/m различных ионов, Ф. Астон назвал
масс-спектрографом.