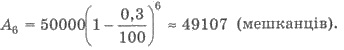АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел И. ЧИСЛА И ВЫРАЖЕНИЯ

§25. ПРОЦЕНТЫ.

5. Формула сложных процентов.

Начальный капитал А₀, положены в банк под р% годовых, через n лет станет наращенными капиталом А_n , вычисляется по формуле:

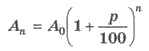
Эту формулу называют формулой сложных процентов.

Процентные деньги (прибыль вкладчика) можно найти как разницу А_n - А₀.

Пример 1. Вкладчик положил в банк 10000 грн. под 16% годовых. Сколько денег будет на счете вкладчика через 2 годы? Сколько процентных денег получит вкладчик через 2 года?

Решения. А₀ = 10000 ; р = 16%; n = 2 . Имеем

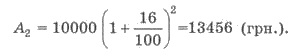
Вкладчик получит такое количество процентных денег

А₂ - А₀ = 13456 -10000 = 3456 (грн.).

По формуле сложных процентов можно решать также задачи, не связанные с наращиванием капитала.

Пример 2. Население некоторого города составляет 50000 жителей. Каждый год население уменьшается на 0,3%. которым будет население этого города через 6 лет?

Решения. Поскольку население города ежегодно уменьшается на один и тот же процент, и этот процент к количества населения предыдущего года, а не до исходного количества жителей, то можно использовать формулу сложных процентов.

Имеем А₀ = 50000; р = -0,3 (поскольку население уменьшается, то г 0); n = 6.

Тогда