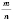
Рациональные числа - это числа, которые могут быть записаны в виде , где m - целое число, n - натуральное.
Каждое рациональное число можно представить в виде бесконечной периодической десятичной дроби. И наоборот, каждый бесконечная периодическая десятичная дробь является рациональным числом.
Числа, которые изображаются бесконечными неперіодичними десятичными дробями, называют иррациональными.
Рациональные и иррациональные числа образуют множество действительных чисел.
Обозначения:
множество натуральных чисел - N;
множество целых чисел - Z;
множество рациональных чисел - Q;
множество действительных чисел - R.
Обратите внимание: каждое натуральное число является целым, каждое целое - рациональным, каждое рациональное - действительным.
Примеры иррациональных чисел:
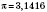
...; 0,12345...; 10,1010010001...; ...
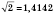
Действительные числа можно складывать, вычитать, умножать, возводить в степень и делить (делить на числа, отличные от 0). Все известные свойства действий остаются такими же.