2-й семестр

МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

1. Свойства газов, жидкостей, твердых тел

Урок 7/78

Тема. Основное уравнение МКТ идеального газа

Цель урока: выяснить механизм давления идеального газа и его зависимость от микропараметров

Тип урока: изучение нового материала

План урока

ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА

1. Основное уравнение молекулярно-кинетической теории идеального газа

Основная задача молекулярно-кинетической теории газа заключается в том, чтобы установить соотношение между давлением газа и его микроскопическими параметрами - массой молекул, их средней скоростью и концентрацией. Это соотношение называется основным уравнением молекулярно-кинетической теории газа.

Поскольку давление газа на стенку сосуда обусловлено ударами молекул, давление газа пропорционально концентрации молекул n: чем больше молекул в единице объема, тем больше ударов молекул о стенку за единицу времени. Каждая молекула при ударе о стенку передает ей импульс, пропорциональный импульсу молекулы, равном по модулю m0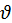, где 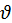- модуль скорости молекулы. Поэтому можно было бы ожидать, что давление пропорционально nm0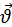, где 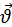- среднее значение модуля скорости молекул.

Однако, на самом деле давление пропорционально не первой, а второй степени скорости, так как, чем больше скорость молекулы, тем чаще она бьется о стенку сосуда. И действительно, расчеты показывают, что основное уравнение молекулярно-кинетической теории идеального газа имеет вид:

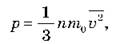
где m0 - масса одной молекулы газа, n - концентрация молекул, 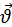2 - среднее значение квадрата скорости молекул.

Коэффициент 1/3 обусловлен трехмерностью пространства - тем, что во время хаотического движения молекул все три направления равноправны.

Итак, немецкий физик Г. Клаузиус выяснил, что давление идеального газа прямо пропорционально концентрации частиц, массы частицы и среднего значения квадрата скорости частицы.

Полученное уравнение связывает макроскопічну величину - давление,- что может быть измерено манометром, с микроскопическими величинами, характеризующими молекулы, и является как бы мостиком между двумя мирами: макроскопическим и микроскопическим.

2. Связь давления со средней кинетической энергией молекулы

Если через 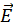обозначить среднюю кинетическую энергию поступательного движения молекулы, 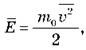то уравнение Клапейрона можно записать в виде:

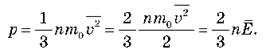
Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы В этой формуле концентрация частиц характеризует число ударов молекул о поршень, а средняя кинетическая энергия молекул определяет интенсивность одного удара.

Вопрос к ученикам во время изложения нового материала

1. Каков механизм возникновения давления газа с точки зрения молекулярно-кинетической теории строения вещества?

2. Почему можно считать, что молекулы в газе движутся только вдоль трех взаимно перпендикулярных направлений?

3. В каких слоях атмосферы воздух по своим свойствам приближается к идеальному газу: у поверхности Земли или на далеких высотах?

ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА

1). Тренируемся решать задачи

Кислород находится в нормальных условиях. Вычислите среднюю квадратичную скорость молекул газа.

Решение

При нормальных условиях давление кислорода равна 1,01·105 Па, а плотность - 1,43 кг/м3. Считая, что концентрация газа n = N/V, можно записать:

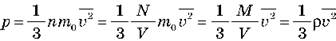
Отсюда получаем: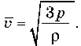

Проверив единицы величин и выполнив расчеты, получаем 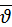= 460 м/с.

2. Определите кинетическую энергию хаотического поступательного движения всех молекул любого газа в баллоне объемом 5 л с давлением 1 МПа.

3. Чему равна средняя кинетическая энергия хаотического движения молекул аргона, если 2 кг его, находясь в сосуде объемом 2 м3, оказывают давление 3·105 Па?

2). Контрольные вопросы

1. Каким образом в основном уравнении молекулярно-кинетической теории мы получили множитель 1/3?

2. Почему молекула при столкновении со стенкой сосуда действует на нее с силой, пропорциональной скорости, а давление пропорционально квадрату скорости?

3. Как средняя кинетическая энергия молекул зависит от концентрации газа и его давления на стенки сосуда?

Что мы узнали на уроке:

• Давление идеального газа прямо пропорционально концентрации частиц, массе частицы и среднему значению квадрата скорости частицы.

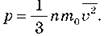
• Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы:

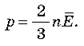
Домашнее задание

1. Конспект.

2. Решите задачи:

г1): 1. Как изменится давление газа, если концентрация его молекул увеличится в 3 раза, а средняя квадратичная скорость молекул уменьшится в 3 раза?

2. Под каким давлением находится газ в сосуде, если средняя квадратичная скорость его молекул 103 м/с, концентрация молекул 3·1025 м-3, а масса каждой молекулы 5·10-26 кг?

3. Определите среднюю кинетическую энергию поступательного движения молекул газа с давлением 105 Па. Концентрация молекул газа 2,7·1025 м-3.

р2): 1. Определите плотность кислорода, находящегося под давлением 1,3·105 Па. Средняя квадратичная скорость молекул 1,4·103 м/с.

2. Какое давление на стенки сосуда оказывают молекулы газа, если масса газа 3 г, объем 5·10-4 м3, средняя квадратичная скорость молекул 500 м/с?

3. Какова средняя квадратичная скорость движения молекул газа, который занимает объем 5 м3 с давлением 2·105 Па и имеет массу 6 кг?

Г3): 1. Давление углекислого газа, если в баллоне объемом 40 л содержится 5·1024 молекул, а средняя квадратичная скорость молекул 400 м/с?

2. Определите кинетическую энергию хаотического поступательного движения всех молекул любого газа в баллоне объемом 10 л и давлением 4·105 Па.

3. Часть стенки сосуда покрыли клеем, что поглощает все падающие молекулы газа. Изменится ли давление газа на этот участок стенки? Обоснуйте свой ответ.