Часть 2 МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

Раздел 7 ОСНОВЫ ТЕРМОДИНАМИКИ

7.12. Третий принцип термодинамики. Отрицательные температуры

В 1906 г. принципы термодинамики было дополнено тепловой теоремой Нернста. Эта теорема не вытекает из первого и второго принципов, а выражает новый закон природы, поэтому ее часто называют третьим принципу термодинамики. Суть его заключается в том, что при абсолютном нуле температур любые изменения состояния происходят без изменения энтропии, или нулевая изотерма совпадает с нулевой адіабатою. Ведь при абсолютном нуле равновесная система находится в определенном едином состоянии с наименьшей энергией Е₀. Термодинамическая вероятность W такого состояния равна единице. Однако из формулы Больцмана (7.36) следует, что при Т = 0 W = 1, а энтропия S = 0.

Теорема Нернста приводит к выводу, что нельзя достичь температуры абсолютного нуля. С помощью современной техники можно получить низкие температуры около 10~⁵ К. Недостижимость абсолютного нуля температуры приводит лишь к невозможности перехода от положительных до отрицательных абсолютных температур. Однако теорема Нернста не исключает возможности существования наряду с положительными отрицательных абсолютных температур.

Если исходить из того, что температура пропорциональная средней кинетической энергии частиц, то для атомных систем, которым свойственна лишь кинетическая энергия движения частиц, отрицательная температура не имеет физического содержания. Кроме молекулярно-кинетического толкование температуры ее рассматривают как величину, что определяет распределение частиц с энергиями. Если воспользоваться этим более общим вопросом температуры, то придем к выводу о существование и отрицательных температур.

Если газ находится в каком-то силовом поле, а следовательно, его частицам присуща некоторая потенциальная энергия, то количество частиц, имеющих определенную энергию 17, определяют по формуле

Выражение (7.37) называют формулой Больцмана. С помощью этой формулы можно определить относительное количество частиц, имеющих в условиях теплового равновесия энергию U:

С формулы (7.38) видно, что относительное количество n / n₀ частиц с энергией U зависит не только от этой энергии, но и от температуры. Поэтому температуру используют как величину, что обуславливает распределение частиц с энергиями. Из формулы (7.38) видно, что чем больше U, тем меньше относительное количество частиц n / n₀, которые имеют эту энергию. Понятно, что в равновесном состоянии, для которого справедливый закон Больцмана, n всегда меньше n₀. Логарифмуючи равенство (7.38), достанем

откуда

Следовательно, если n n₀, то Т > 0. Для атомной системы, в которой n может быть и больше n₀, температура может быть также отрицательной, поскольку при n > n₀ Т становится отрицательной.

Условия реализации такого случая легче понять, если рассмотреть не классическую систему, где отрицательная температура не может быть реализована, а квантовую и воспользоваться понятием энтропии, что определяет степень хаоса в системе.

При абсолютном нуле температур все частицы системы находятся на своих обычных энергетических уровнях, а все остальные уровни пусты. Система в таких условиях максимально упорядочена, и ее энтропия равна нулю (равен нулю и ее теплоемкость).

В случае увеличения температуры системы предоставлением ей энергии частицы будут переходить также на высшие уровни энергии. При этом чем выше температура, тем больше «населенность» более высоких энергетических уровней. Распределение частиц на энергетических уровнях определяют по формуле Больцмана (7.37). «Расселение» частиц на многих уровнях увеличивает, конечно, хаос в системе, и ее энтропия возрастает с повышением температуры. Наибольший хаос, а следовательно, и максимум энтропии соответствовали бы такому распределению частиц с энергиями, когда они равномерно распределялись на всех энергетических уровнях. Такое распределение означал бы, что в формуле (7.37) n = n₀ и, следовательно, Т = ∞. Таким образом, равномерное распределение частиц с энергиями соответствует бесконечно высокой температуре и максимальной энтропии.

Если предоставить системе, что уже находится при бесконечно высокой температуре, дополнительную энергию, то частицы вынуждены будут подниматься на более высокие энергетические уровни, а это приведет к того, что «заселенность» этих уровней будет больше от самого низкого уровня. Такое преимущественное накопление частиц на более высоких уровнях уже некотором благоустройству сравнению с тем полным хаосом, который был при Т = ∞, т.е. при равномерном распределении частиц с энергиями. Энтропия достигает максимума при T = ∞, начинает уменьшаться при дальнейшем оказании системе энергии. Однако если со ростом энергии энтропия системы не увеличивается, а уменьшается, то это означает, что температура ее не положительная, а отрицательная.

Чем больше энергия подводится к системы, тем больше частиц окажется на самых высоких энергетических уровнях. В предельном случае можно представить состояние, когда все частицы соберутся на высочайших уровнях. Такое состояние, очевидно, также является полностью упорядоченным, и его энтропия равна нулю. Поэтому температуру, при которой устанавливается этот полностью упорядоченное состояние, обозначают через -0, в отличие от обычного абсолютного нуля (+0) (рис. 7.7).

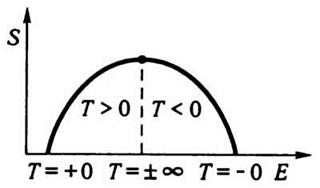
Рис. 7.7

Различие между этими двумя нулями заключается в том, что к первому из них мы подходим со стороны отрицательных, а до второго - со стороны положительных температур.

Итак, возможные температуры системы не ограничиваются интервалом от абсолютного нуля до бесконечности, а распространяются от +0 до +∞, - ∞ до -0, к тому же +∞ и -∞ совпадают друг с другом. С точки зрения упорядоченности, а следовательно, и энтропии возможны следующие три состояния:

1. Полное благоустройство - частицы сконцентрированы на самых низких уровнях энергии. Это состояние соответствует «обычному» абсолютному нулю температур (+0).

2. Полный хаос - частицы равномерно распределены на всех энергетических уровнях. Этому состоянию соответствует температура ±∞.

3. Полное благоустройство - частицы занимают только высокие энергетические уровни. Температуре, соответствующей этому состояния, приписывают значение-0.

Существует очень важное различие между этими двумя упорядоченными состояниями с температурами +0 и-0. Состояние «обычного» абсолютного нуля, если его можно было бы создать в системе, является состоянием устойчивой равновесия, из которого система сама по себе, без вмешательства извне, не может выйти. Это связано с тем, что энергия системы в таком состоянии приобретает минимального значение.

Состояние отрицательного абсолютного нуля является состоянием слишком неравновесным, поскольку в этом случае энергия системы максимальна. Если можно было бы привести систему в такое состояние, а потом оставить ее саму на себя, то она сразу вышла бы из этого неравновесного, неустойчивого состояния. Его можно было бы сохранить, только непрерывно предоставляя системе энергию. Без этого частицы, размещаемые на высших энергетических уровнях, обязательно переходить на низшие уровни.

Общим свойством обеих «нулей» является недосягаемость их: для достижения их надо затратить бесконечно большую энергию.

Неустойчивым, неравновесным является не только состояние, что соответствует температуре -0, а все состояния с отрицательными температурами. Всем им соответствуют значения n > n₀, а для равновесия требуется обратное соотношение n и n₀ (n n₀).

Следует отметить, что атомные системы, в которых возможны состояния с отрицательными температурами, - это не только умозрительная теоретическая построение. Такие системы реально существуют, и в них можно осуществить отрицательные температуры. Излучение, возникающее при переходе из состояния с отрицательной в состояние с обычной температурой, практически используют в специальных приборах - молекулярных генераторах и усилителях (мазерах и лазерах), о которых речь пойдет в подразделе 15.13.