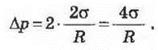МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
4. СВОЙСТВА ЖИДКОСТЕЙ
4.4. ФОРМУЛА ЛАПЛАСА
Формула Лапласа. Дополнительное давление, который обусловлен
кривиною поверхности жидкости, определяется так:
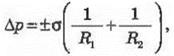
где
R1 и R2 - радиусы кривизны двух взаимно
перпендикулярных сечений поверхности жидкости; знак «+» - для выпуклого мениска, «-»
- вогнутого.
Давление в точках А и А' указанный на
рис. 17:
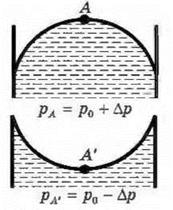
Рис. 17
ρ0 - давление на свободную
поверхность.
Если R1 = R2 =
R (сферическая поверхность), то
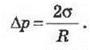
Для тонкостенной полой сферы
(пузырьки), что имеет две поверхности - внешнюю и внутреннюю - лапласів давление
равна: