МАТЕМАТИКА
ВЕКТОРЫ
Векторы в пространстве
Вектор - направленный отрезок 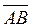
А - начало вектора
В - конец вектора
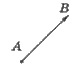
Модуль вектора - длина отрезка,
изображающий вектор: |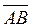 |.
|.
Два вектора равны, если они
одинаково направлены и имеют равные модули.
Координаты вектора с началом в
точке А(x1,y1,z1) и концом В точке В(х2,у2,z2).
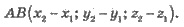
Равные векторы имеют равные соответствующие
координаты.
Коллинеарны векторы - ненулевые
векторы, лежащие на одной прямой или на параллельных прямых 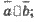
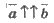 - одинаково направленные векторы
- одинаково направленные векторы 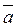 и
и 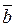 ;
;
 - противоположно направленные векторы
- противоположно направленные векторы 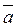 и
и 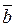 .
.
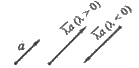
Теорема: Если 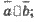 , то существует число λ, такое, что
, то существует число λ, такое, что 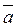 = λ
= λ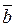 . Если λ
> 0, тогда
. Если λ
> 0, тогда 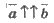 . Если λ
0, тогда
. Если λ
0, тогда  .
.
Действия с векторами
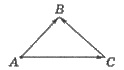
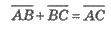 - правило треугольника
- правило треугольника
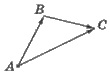
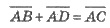 -
правило параллелограмма
-
правило параллелограмма
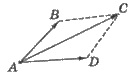
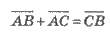
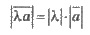
Суммой векторов 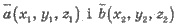 является
вектор
является
вектор 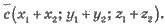
Произведением вектора 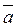 (х, у, z) на число λ является вектор
(х, у, z) на число λ является вектор 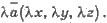
Свойства: 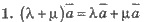
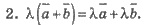
Скалярным произведением векторов 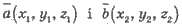 является число
является число
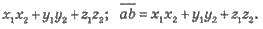
Скалярный квадрат вектора 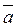 (х, у, z)
(х, у, z)
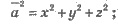 откуда
откуда 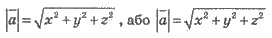
Теорема: Скалярное произведение двух
ненулевых векторов равно произведению их модулей на косинус угла между ними.
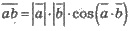
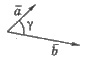
Если 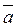
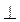
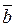 , тогда
, тогда 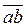 =
0.
=
0.
Если 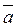 ·
· 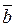 = 0 и
= 0 и 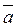 ≠ 0,
≠ 0, 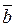 ≠ 0, тогда
≠ 0, тогда 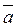
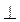
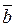
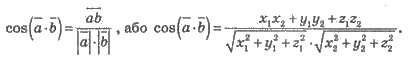
Уравнение плоскости
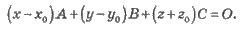
где (х0, у0, z0) -координаты точки, через которую
проходит плоскость;
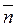 (А; В; С) - нормальный вектор к
плоскости
(А; В; С) - нормальный вектор к
плоскости