УРОКИ № 68, 69
Тема. Анализ итоговой контрольной работы. Решение интересных задач
Задачи повышенной сложности
1. При каких значениях а уравнение не имеет действительных корней?
1) х2 + 4х - а = 0;
2) (а - 1)х2 + (2а - 3)х + а = 0;
3) (а - 2)х2 - 2(а - 3)х + а + 1 = 0;
2х2 + (2а + 12)х + а2 + 2а + 26 = 0.
2. Решите неравенство:
1) ах > 0;
2) ах 1;
3) ах ≥ а;
4) а2х ≤ 0;
5) а + х 2 - ах;
6) 2(х - а) ах - 4;
7) (a - 2)x > a2 - 4;
8) (а + 3)х ≤ а2 - 9.
3. Решите систему неравенств:
1) 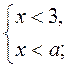 2)
2) 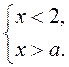
4. Решите неравенство:
1) |х + 2| + 3 ≥ 5;
2) |х - 6| - 7х 18;
3) |х + 1| + |х - 1| ≤ 2.
5. Докажите, что:
1) (а + b) 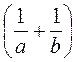 ≥ 4, если а > 0, b > 0;
≥ 4, если а > 0, b > 0;
2) (а + 6)(b + 3)(с + 2) ≥ 48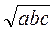 , если а ≥ 0; b ≥ 0; c ≥ 0;
, если а ≥ 0; b ≥ 0; c ≥ 0;
3) 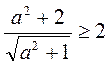 при всех действительных значениях а.
при всех действительных значениях а.
6. Дано функцию: 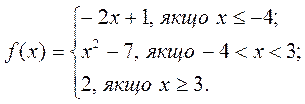 Найдите f (-5); f (-2); f (3); f (7,6). Постройте график этой функции.
Найдите f (-5); f (-2); f (3); f (7,6). Постройте график этой функции.
7. Найдите область определения функции 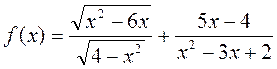 .
.
8. Выполнив геометрические преобразования графиков элементарных функций, постройте график функции:
1) у = 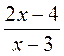 ;
;
2) у = |х2 - 3|;
3) y = х2 - 6|х| + 5.
9. Парабола, что является графиком квадратичной функции у = ах2 + bх + с, имеет вершину в точке М(2; 1) и проходит через точку К(-1; 5). Найдите значения коэффициентов a, b и с.
10. Постройте график функции:
1) у = 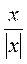
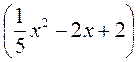 ;
;
2) у = х2 - 5х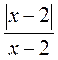 - 14.
- 14.
11. Пусть х1 и х2 - нули квадратичной функции y = 4x2 - (3a + 2)x + а - 1. Найдите, при каких значениях а выполняется неравенство x1 3 x2.
12. Решите неравенство:
1) х2 - (а + 3)х + 3а 0;
2) х2 + (1 - 3а)х + 2а2 - 3а - 2 > 0.
13. Найдите решения неравенства:
1) |х2 - х - 3| 9;
2) |х2 + 5x| > 6;
3) |х - 4|(х + 2) > 4х;
4) x2 - 4|x| 12.
14. Постройте график уравнения:
1) |2х - у| = 5;
2) х2 + 7у2 = 0;
3) |х| + |у| = 5;
4) у = 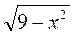 .
.
15. Сколько решений в зависимости от а имеет система уравнений:
1) 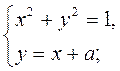 2)
2) 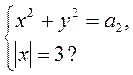
16. Докажите, что если a, b и с - три последовательные члены арифметической прогрессии, то a2 + 8bc - (2b + c).
17. Решите уравнение:
1) 5 + 9 + 13 + ... + 4n + 1 = 324;
2) 4 + 10 + 16 + ... + х = 310.
18. Группа учащихся принимала участие в лыжном кроссе. Количество учащихся, выполнивших норматив, оказалась от 94,2% до 94,4%. Какова наименьшая возможная количество учащихся принимала участие в кроссе?
19. В сосуде объемом V л содержится г-процентный раствор соли. Из сосуда выливают а л смеси и доливают столько же воды, образовавшийся раствор перемешивают. Такую процедуру повторяют 5 раз. Найдите процентное содержание соли в образовавшемся растворе.
Интересные (логические) упражнения
1. Вставьте пропущенное число:
в = 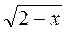 |
x 2 |
в = 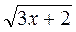 |
? |
2. Вставьте пропущенные неравенства, числовые промежутки, выражения или изображения.
3. Который квадратный трехчлен из данных надо выбрать?
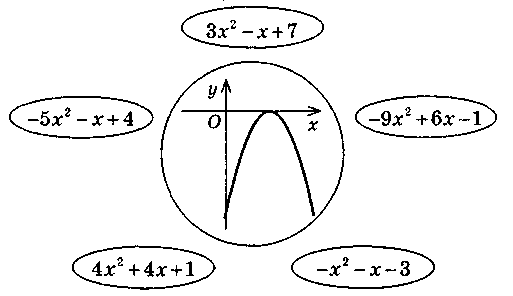
4. Вставьте пропущенные числа, выражения, неравенства, слова или рисунки.
1) |
у = х + 1 |
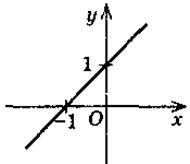
|
|
в = 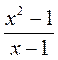 |
? |
|
|
|
2) |
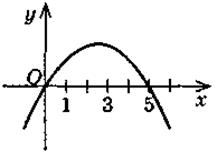
|
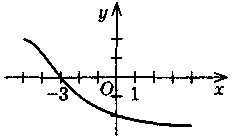
|
|
[0; 5] |
? |
|
|
|
3)
|
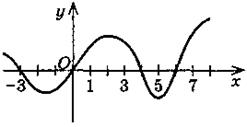
|
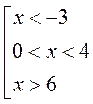
|
|
у = 3 - 2х |
? |
|
|
|
4)
|
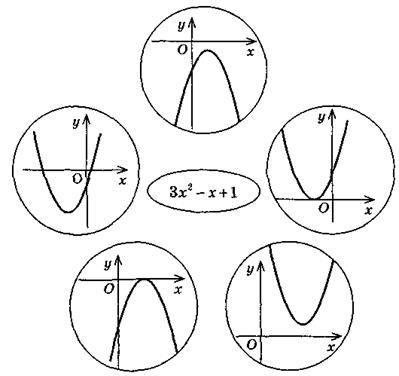
|
|
|
5) |
РАКЕТА |

|
РЕКА |

|
СОН ? |
6)
|
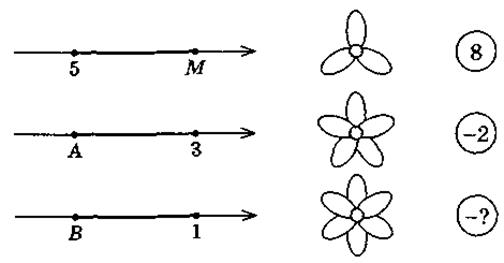
|
7) |
(х - 2)(х + 1) -∞ х +∞; 2 х +∞ (5 - х)(х - 1) ? |
|
|
8) |
ах - 3 = х |
1 |
|
7х - b = тх |
7 |
|
bх + 2 = 3х |
? |
|
|
9) |
x2 - x - 12 |
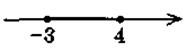
|
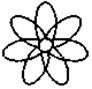
|
|
х2 - 2x - 3 |
? |
? |