МЕХАНИКА

1. ОСНОВЫ КИНЕМАТИКИ

1.2. ОПЕРАЦИИ С ВЕКТОРНЫМИ ВЕЛИЧИНАМИ

Вектор - направленный отрезок. Векторные величины имеют числовое значение (модуль), направление, точку приложения (рис. 3).

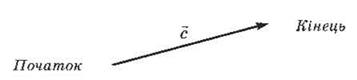
Рис. С

Проекция вектора 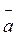на ось Х - длина отрезка, соединяющий проекцию начала вектора на ось Ох с проекцией конца вектора на ту самую ось. Она равна произведению модуля

этого вектора на косинус угла между направлением оси и вектора.

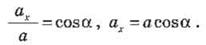
Проекция вектора может быть положительной, отрицательной и равна нулю.

Если угол между направлением вектора и осью острый, то 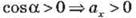(рис. 4, а).

Если угол между направлением вектора и осью тупой, то 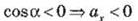(рис. 4, б).

Если угол между направлением вектора и осью прямой 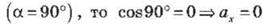(рис. 4, в).

Модуль векторной величины можно определить через проекции вектора на оси Ох и Оу (рис. 4, г):

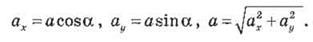
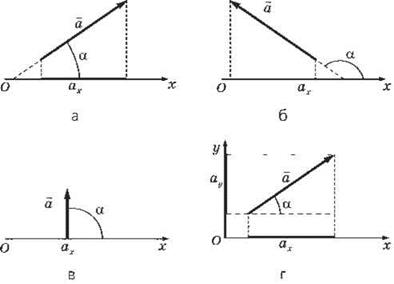
Рис. 4

При умножении векторной величины на скаляр одержуймо вектор, колінеарний данном:

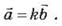
Сложение векторов по правилу треугольника: параллельным переносом сочетается начало второго вектора с концом первого, начало третьего-с концом второго и т. д.; тогда сумма векторов - это вектор, соединяющий начало первого вектора с концом последнего.

На рис. 5, а изображена добавление двух векторов по правилу треугольника:

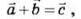
на рис. 5, б - сложение трех векторов по правилу треугольника:

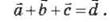
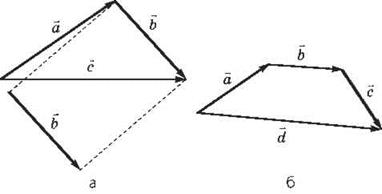
Рис. 5

Сложение векторов по правилу параллелограмма: параллельным переносом совмещаются начала двух векторов; тогда сумма векторов - диагональ, построенная на этих векторах как на сторонах параллелограмма.

На рис, 6, а показано сложение двух векторов по правилу параллелограмма, на рис. 6, б - сложение трех векторов по правилу параллелограмма.

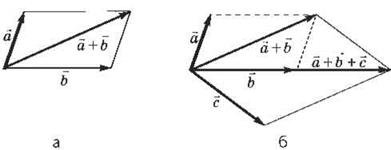
Рис. 6

Вычитание векторов по правилу треугольника: совмещаются начала двух векторов; тогда разность векторов - это вектор, соединяющий их концы. Он обращен в сторону уменьшаемого вектора.

На рис. 7 показано вычитание двух векторов по правилу треугольника:

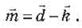
Рис. 7

Проекция суммы векторов на координатную ось равна сумме проекций слагаемых векторов на ту же ось (рис. 8):

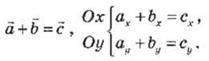
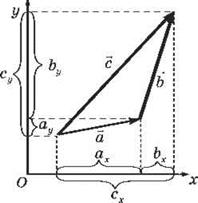
Рис. 8