ГЕОМЕТРИЯ
Раздел ІІ. СТЕРЕОМЕТРИЯ
ОБРАЗЦЫ ТЕСТОВЫХ ЗАДАНИЙ.
Задания с выбором одного правильного
ответы.
Задача 1-60 имеют по пять
вариантов ответа, среди которых только один правильный.
1. Какие из приведенных утверждений
правильные?
I. Если круг имеет с плоскостью две
общие точки, то все точки окружности принадлежат действий плоскости.
II. Если две вершины трапеции
принадлежат плоскости, то все точки этой трапеции принадлежат плоскости.
III. Если
три вершины квадрата принадлежат плоскости, то все точки этого квадрата принадлежат
плоскости.
2. Заданы две параллельные прямые а и b. Сколько существует различных плоскостей,
проходят через прямую b, параллельную прямой а?
3. Укажите все правильные утверждения.
I. Через точку М, что не принадлежит
плоскости а , можно провести лишь одну прямую, параллельную α.
II. Через точку М, не принадлежащую плоскости
а , можно провести лишь одну прямую, перпендикулярную α.
III. Через
точка М не принадлежит плоскости а , можно провести лишь одну плоскость,
параллельную α.
IV. Через
точка М не принадлежит плоскости а , можно провести лишь одну плоскость,
перпендикулярную α.
4. На рисунке 522 куб АВСDА1В1С1D1. Укажите среди приведенных ниже прямую,
что образует с прямой DС1 пару мимобіжних
прямых.
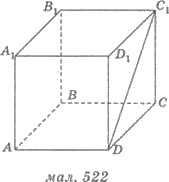
5. На рисунке 522 прямоугольный
параллелепипед АВСDА1В1С1D1. Укажите среди приведенных ниже
плоскость, которая является перпендикулярной к плоскости АА1D.
6. АВСDА1В1С1D1
- куб (рис. 522). Найти угол между скрещивающимися прямыми ВС и DС1.
7. АВСDА1В1С1D1
- прямоугольный параллелепипед (рис. 522). АD = 4 см, DС
= 3 см, DD1 = 2 см. Найти расстояние от прямой DD1 к плоскости АА1С1.
8. АВСDА1В1С1D1
- куб (рис. 522) с ребром 4 см. Найти расстояние
от точки А до плоскости ВВ1D.
9. Линейный угол двугранного угла
равна третьей части развернутого угла. Чему равна градусная мера
двугранного угла?
10. Сколько
граней у дванадцятикутній призме?
11. Сколько
ребер имеет вісімнадцятикутна пирамида?
12. Угол
между любыми соседними боковыми ребрами правильной пирамиды равен 90º. Какой многоугольник может быть основой
пирамиды?
13. Площади
трех граней прямоугольного параллелепипеда соответственно равны 6
см2, 8 см2
и 12 см2. Найти площадь полной поверхности прямоугольного параллелепипеда.
14. Диагональным
сечением правильной четырехугольной призмы является прямоугольник, площадь которого равна 20
см2. Периметр основания призмы равна 8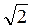
см. Найти высоту
призмы.
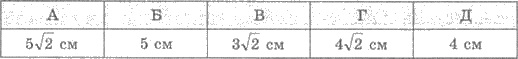
15. Площадь полной поверхности куба
равна 54 см2. Найти объем куба.
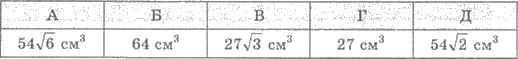
16. Найти площадь диагонального
сечения куба, ребро которого равно 1 см.
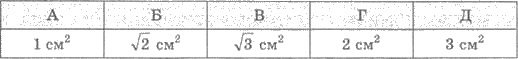
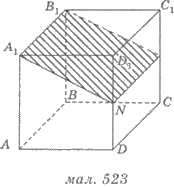
17. В
кубе АВСDА1В1С1D1 точка N - середина ребра NN1 (рис. 523). Через прямую А1В1 и точку N проведена сечение. Найти
площадь сечения, если ребро куба равно 2 см.
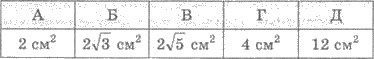
18. Найти
длину диагонали прямоугольного параллелепипеде, измерения которого равны 1 см, 2
см, 3 см.
19. Периметр
боковой грани правильной треугольной призмы равна 24 см. Найти площадь боковой
поверхности призмы, если сторона основания равна 3 см.
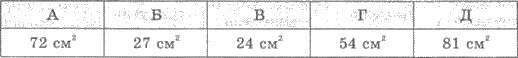
20. Ширина
прямоугольного параллелепипеда равна 3 см, а длина - 6 см. Найти высоту
прямоугольного параллелепипеда, если она на 5 см короче диагональ.
21. Найти
площадь боковой поверхности правильной четырехугольной пирамиды, сторона основания которой
равна 6 см, а анофема - 8 см.
22. Сколько
сторон имеет многоугольник, лежащий в основании призмы, если она имеет 36 ребер.
23. Высота
наклонной призмы вдвое короче боковое ребро. Какой угол образует высота призмы с
этим боковым ребром?
24. Стороны
основания параллелепипеда равны 3 см и 8 см, а угол между ними 60°. Найти площадь
диагонального сечения параллелепипеда, если его высота равна 10 см.
25. Основой
прямого параллелепипеде является ромб со стороной 2
см и тупым углом 120°. Меньшая диагональ
параллелепипеда наклонена к плоскости основания под углом 60°. Найти высоту
параллелепипеда.
26. Площадь основания четырехугольной
пирамиды равна 16 см2, а площадь одной боковой грани 12 см2.
Найти апофему пирамиды.
27. Сторона
основы правильной треугольной пирамиды равна 4 см, а высота - 5
см. Найти площадь
сечения пирамиды, проходящего через ее высоту и боковое ребро.
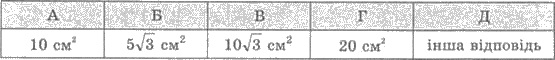
28. Боковое
ребро правильной четырехугольной пирамиды равно 4 см и образует угол 30° с плоскостью основания.
Найти сторону основания пирамиды.
29. Диагональ куба равна 2 см. Найти его площадь
полной поверхности.
30.
Объем правильной
четырехугольной призмы равна 80 см3, а ее высота равна 5
см. Найти длину
стороны основания призмы.
31. Стороны
основания прямого параллелепипеда равны 2л/с" см и 4 см и образуют угол
60°. Найти объем параллелепипеда, если его боковое ребро равно 5 см.
32. Стороны
основы прямоугольного параллелепипеде равны 3 см и 4 см, а диагональ большей
по площади боковой грани равна 5 см. Найти объем параллелепипеда.
33. Сторона
основы правильной треугольной призмы равна 6 см, а ее объем - 54 см3. Найти
высоту призмы.
34. Классные
помещения должны быть рассчитаны так, чтобы на одного ученика было не менее 6 м3
воздуха. Какое наибольшее количество учеников можно разместить в классном помещении,
что имеет форму прямоугольного параллелепипеда с измерениями 8 м, 4,5 м и 3 м без
нарушение санитарных норм?
35. В
сколько раз объем куба с ребром 1 м больше объема куба с ребром 50 см?
36. Прямоугольник
со сторонами 4 см и 5 см вращается вокруг большей стороны. Найти площадь
диагонального сечения цилиндра.
37. Осевым
сечением цилиндра является прямоугольник, диагональ которого равна 12 см. Найти высоту
цилиндра, если диагональ осевого сечения наклонена к плоскости основания под углом
60°.
38. Высота
цилиндра вдвое больше его радиус. Отрезок, соединяющий центр верхнего
основы с точкой окружности нижнего основания равна 4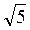
см. Найти высоту цилиндра.
39. Площадь
боковой поверхности цилиндра равна 40π см2, а площадь основания - 16π см2. Найти высоту цилиндра.
40. Радиус
основания цилиндра равен 4 см, а высота - 3 см. Найти площадь полной поверхности
цилиндра.
41. Периметр
осевого сечения цилиндра равна 36 см. Найти площадь боковой поверхности
цилиндра, если его высота равна 8 см.
42. На рисунке изображен 524
развертку цилиндра. Найти объем цилиндра.
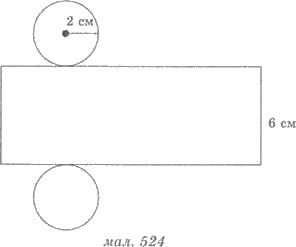
43. Найти объем тела, образованного
обращением куба вокруг своего ребра, длина которого равна 2 см.
44. Радиус основания конуса равен 2
см, а образующая образует с высотой угол 45°. Найти площадь осевого сечения конуса.
45. Диаметр
основания конуса в 2
раз больше его высоту. Найти градусную меру угла между образующей конуса и
плоскостью его основания.
46. Образующая
усеченного конуса равна 10 см, а диаметры оснований 6 см и 18 см. Найти высоту
усеченного конуса.
47. Диаметр основания конуса равен 4
см и образует с образующей угол 60º. Найти площадь боковой поверхности
конуса.
48. Объем цилиндра равен 24 см3.
Найти объем конуса, радиус основания которого равен радиусу основания цилиндра, а
высота вдвое больше высоты цилиндра.
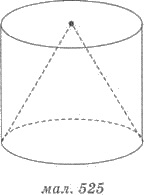
49. С
деревянного цилиндра выточены конус так, что его основание совпадает с одной из
оснований цилиндра, а вершина - с центром другого основания цилиндра (рис. 525). Найти отношение объема
сточеної части цилиндра до первоначального объема цилиндра.
50. Сферу, радиус которой равен 10 см пересечена плоскостью на
расстоянии 8 см от центра сферы. Найти длину линии, по которой плоскость пересекает
сферу.
51. Объем шара равен 36π см3. Найти ее диаметр.
52. Основой прямой призмы является ромб со
стороной 8 см и острым углом 30º. Найти площадь поверхности сферы,
вписанного в эту призму.
53. Найти расстояние от точки
М(3;4;-5) к плоскости ху.
54. Ортогональной проекцией отрезка
МN с концами в точках М(2;-1;3) и N(-1;-1;3) на плоскость вz являются:
55. Найти расстояние от точки
Р(3;4;6) к оси z.
56. На оси ординат найти точку,
расстояние от которой до точки В(4;1;8) равна 12.
57. Дано векторы
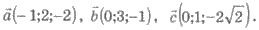Какое из утверждений правильное?
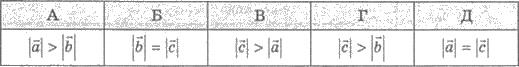
58. Найти вектор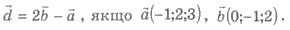 
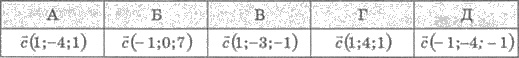
59. При каких значениях у и z векторы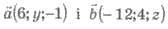 
коллинеарны?
60. При каком значении m векторы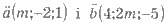 
перпендикулярны?
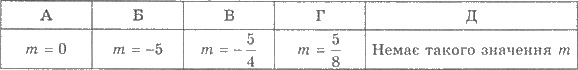
Задания на установление
соответствий.
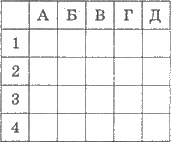
В заданиях 1-5 к каждому из
четырех строк информации, обозначенных цифрами, выберите один правильный, на
Вашему мнению, вариант, обозначенный буквой.
1. На рисунке изображен 526
прямоугольный параллелепипед АВСDА1В1С1D1, АВ = 1, АD = 2, АА1
= 2. Установить соответствие между геометрическими величинами (1-4) и их
числовыми значениями (А-Д).
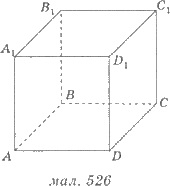
1 Расстояние между скрещивающимися прямыми
АА1 и DС.
2 Длина диагонали прямоугольного
параллелепипеда.
3 Площадь полной поверхности прямоугольного
параллелепипеда.
4 Объем прямоугольного
параллелепипеда.
А 16.
Бы 12.
В 4.
Г 3.
Д 2.
2. На рисунке 526 изображен куб АВСDА1В1С1D1. Установить соответствие между
заданными углами (1-4) и их градусными мерами.
1 Угол между прямыми ВВ1 и D1C.
2 Угол между прямыми АС и В1D1
3 Угол между прямыми АВ1 и А1D
4 Угол между прямыми АВ и С1D1
А 0º
Бы 30º
В 45º
Г 60º
Д 90º
3. Установить соответствие между
видами многогранника
(1-4) и общим числом его ребер.
1 Параллелепипед.
2 Правильная двенадцатиугольная пирамида.
3 Шестиугольная призма.
4 Треугольная усеченная пирамида.
А 9
Б 12
В 18
Г 24
Д 30
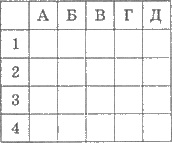
4. На рисунке изображен 527
правильную четырехугольную пирамиду QАВСD, у которой боковое ребро равно 5, а высота - 4.
Установить соответствие между геометрическими вершинами (1-4) и их числовыми
значениями (А-Д).
1 Диагональ основания пирамиды.
2 Площадь основания пирамиды.
3 Площадь диагонального сечения
пирамиды.
4 Объем пирамиды.
А 24
Б 18
В 16
Г 12
Д 6
5. Дано векторы
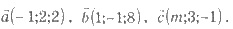Установить соответствие между характеристиками векторов или результатами действий над ними
(1-4) и их численными значениями.
1 Модуль вектора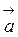 
.
2 Модуль вектора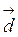 
= - 
.
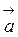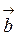3 Скалярное произведение векторов 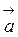и .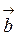
4 Значение m, при котором векторы 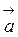и 
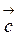перпендикулярны.
А 3
4
В 7
Г 10
Д 13
Задания с кратким ответом.
1. Из точки А к плоскости проведены
две наклонные, каждая из которых равна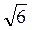 
см. Угол между наклонными - 90°, проекции
наклонных образуют угол 120°. Найти (в см) длины проекций наклонных на плоскость.
2. Точка М удалена от каждой из
вершин рівнобічної трапеции на 65 см. Боковая сторона трапеции перпендикулярна к
ее диагонали. Найти расстояние от точки М до плоскости трапеции, если высота
трапеции равна 24 см, а диагональ трапеции - 40 см.
3. Из точек А и В, которые лежат в двух
перпендикулярных плоскостях α и β
проведены перпендикуляры АК и ВL к прямой пересеку плоскостей. АL = 8 см, КВ = 14 см, LК = 2 см. Найти АВ (в см).
4. Два равнобедренные треугольники имеют
общую основу длиной 20 см. Угол между плоскостями треугольников равен 60º. Площадь одного из треугольников
равен 30 см2, а высота другого,
проведенная к основанию, равна 5 см. Какой наибольшей (в см) может быть
расстояние между вершинами треугольников?
5. Апофема правильной четырехугольной
пирамиды равна 4
см и образует угол 60° с плоскостью основания. Найти (в см3) объем
пирамиды.
6. В основе прямой призмы лежит
прямоугольник, стороны которого относятся как 1 : 3. Площадь боковой поверхности призмы
равна 48 см2, а полной поверхности - 72 см2. Найти (в
см) высоту призмы.
7. Основанием прямого параллелепипеда является
ромб с периметром 20 см и диагональю
6 см. Большая диагональ параллелепипеда равна 10 см.
Найти объем параллелепипеда (в см3).
8. Шар пересекли плоскостью на
расстоянии 15 см от центра. Площадь образованного сечения равна 64 см п2.
Найти (в см) длину большого круга сферы, что ограничивает
данную пулю. В ответ запишите величину l/π, где l - длина
круга.
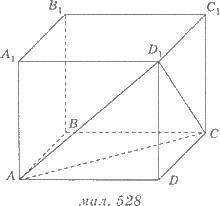
9. На рисунке 528 изображен куб АВСDА1В1С1D1. Вычислите (в см3) объем
этого куба, если объем пирамиды D1АDС равна 8 см3.
10. Комната
имеет форму прямоугольного параллелепипеда. Ширина комнаты - 4 м, длина - 6
м, высота - 3м. Площадь стен комнаты равна 0,75
площади боковой поверхности прямоугольного параллелепипеда. Сколько краски (в кг)
нужно для того, чтобы полностью покрасить стены этой комнаты, если 1 м2
тратится 0,24 кг краски?
11. Высота
конуса равна 6 см, а радиус основания - 8 см. Найти отношение площади основания
конуса к площади его боковой поверхности.
12 В цилиндрической сосуде уровень
воды находится на высоте 36 см. На какой высоте (в см) находится уровень воды,
если перелить ее в цилиндрический сосуд, радиус которой в 2 раза больше радиуса
первой?
13. В
четырехугольную пирамиду, в основе которой лежит равносторонняя трапеция с боковой
стороной 10 см и основами 16 см и 4 см, вписан конус. Все боковые грани пирамиды
наклонены к плоскости основания под углом 60°. Найти площадь поверхности Sбич
конуса (в см2).
В ответ запишите величину S/π.
14. Сторона
основания правильной четырехугольной пирамиды равна 12. Боковое ребро пирамиды
наклонено к плоскости основания под углом 60°. Вычислить площадь S большого круга шара, описанной вокруг
пирамиды. В ответ запишите
величину S/π.
15. Стороны
треугольника равны 13 см, 14 см и 15 см. Шар, объем которого равен (500/3)π см3 касается всех
сторон треугольника. Найти (в см)
расстояние от центра
шара до плоскости треугольника.
16. В
правильную треугольную пирамиду вписали шар, радиус которого равен 2 см. Найти
высоту пирамиды (в см), если она образует угол 30° с апофемою.
17. Задано
вершины треугольника АВС: А(5;0;3), В(9;2;7), С(11;4;15), К - середина АС, L - середина ВС. Найти длину
отрезка КL.
18. Найти
(в градусах) угол С треугольника АВС с вершинами в точках А(5;1;8), В(1;9;0),
С(3;-1;4).
19. Дано: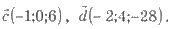 
Найти
модуль вектора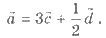 
20. Угол между векторам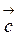и и 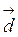равен 120º, 
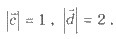Найти 