Криволинейное движение. Равномерное движение материальной точки по окружности. Период и частота. Угловая скорость

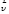
Прямолинейные движения на практике реализуются редко, значительно чаще траекторией материальной точки есть кривая линия. Мгновенная скорость в любой точке траектории при этом направлена вдоль касательной к кривой.

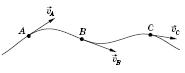
Самым простым из криволинейных движений материальной точки является движение по окружности (в случае вращения тела отдельные его точки описывают окружности).
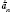
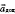
Даже равномерно двигаясь по кругу, материальная точка имеет ускорение, которое характеризует бистроту изменения направления мгновенной скорости в любой точке траектории напрямлене вдоль нормали n к касательной. Именно этим обусловлено одно из названий такого ускорения - нормальное ускорение . Оно направлено к центру круга, в связи с чем называется еще и центростремительным ускорением и вычисляется по формуле .

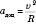
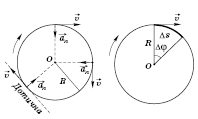
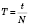
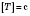
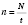
Движение материальной точки по окружности можно характеризовать периодом T и частотой n. Пусть за время t материальная точка совершает N полных обходов окружности. Период - время одного обхода, то есть , , а частота - число обходов в течение секунды, то есть . Очевидно, что , .
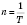
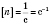
Движение по окружности можно характеризовать также бистротою движения радиуса круга R, проведенного до какого начального положения материальной точки.
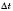
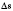
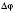
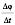
Пусть за время материальная точка прошла по кругу путь (длину дуги окружности), а радиус R обернулся на угол . Этот угол называется угловым перемещением материальной точки. Отношение называется угловой скоростью и обозначается ω (омега),
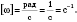
Следовательно, угловая скорость материальной точки численно равна ее угловому перемещению в течение секунды.
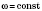
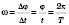
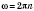
Поскольку при равномерном движении по окружности, то можно рассматривать любое время t и соответствующий угол φ, в частности - период T и полный угол 2π. При этом , или. Выразив центробежная сила ускорение через угловую скорость ω, можно записать так: .
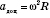