Умножения

Чтобы найти произведение двух чисел с разными знаками, надо перемножить их модули и поставить перед полученным числом знак «-».
Чтобы перемножить два отрицательных числа, надо перемножить их модули (то есть произведение двух отрицательных чисел есть положительное число).
При изменении знака одного из множителей меняется знак всего произведения.
Если произведение содержит четное число отрицательных множителей, он является положительным числом, а если нечетное - отрицательным.
Примеры
1) ;
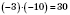
2) ;
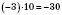
3) ;
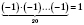
4) .
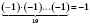
Квадрат любого числа есть число неотрицательное. Например:
; .
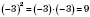
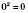
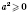
Т.е. для любых значений а.
Знак куба числа совпадает со знаком числа. Например:
;
; .
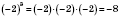
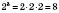
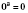
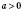
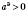
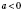
То есть, если , то и ; если , то и .
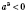
Обратите внимание: ; .
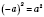
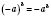
Для умножения рациональных чисел сбываются свойства:
переставная - ;
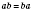
связующее - ;
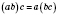
распределительная - ;
.
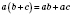
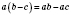
Для любого рационального а правильно:
; ;
.
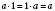
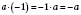
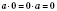
Примеры
1)
.
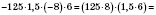
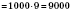
Произведение является положительным, потому что содержит два отрицательных множители.
2) .
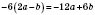
3) .
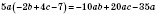
4) Вынести за скобки общий множитель.
а) ;
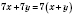
б) ;
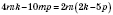
число 2 является НОД (4; 10).
Если буквенный выражение можно записать как произведение числа и одной или нескольких букв, то это число называют числовым коэффициентом выражения. Например:
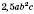
, коэффициент 2,5;
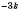
, коэффициент ;
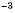
а, коэффициент 1;
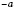
, коэффициент .
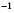
Слагаемые, имеющие одинаковую буквенную часть, называются подобными.
Чтобы свести (т.е. добавить) подобные слагаемые, надо добавить их коэффициенты и результат умножить на общую буквенную часть.
Примеры
1)
;
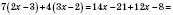
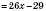
2) .
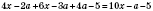