СВОЙСТВА ГАЗОВ, ЖИДКОСТЕЙ, ТВЕРДЫХ ТЕЛ*

Урок № 5

Тема. Идеальный газ. Основное уравнение МКТ

Цель: ознакомить учащихся с уравнением, описывающим свойства веществ в газообразном состоянии.

План урока

1. Модель идеального газа.

2. Давление газа в МКТ.

3. Основное уравнение МКТ идеального газа.

ХОД УРОКА

I. Актуализация опорных знаний

1. Как силы взаимодействия между молекулами зависят от расстояния между ними?

2. Почему газы легко сжимаются?

3. Почему сжать твердые тела, так же, как и жидкости трудно?

II. Изучение нового материала

1. Вы знаете, что расстояния между молекулами газа намного больше размеров самих молекул. Поэтому взаимодействием между молекулами можно пренебречь. Кинетическая энергия молекул намного больше потенциальную энергию взаимодействия. Вместо реального газа, между молекулами которого действуют сложные силы взаимодействия, мы рассмотрим его физическую модель. Эта модель называется идеальным газом.

Идеальный газ - это газ, в котором молекулы можно считать материальными точками, а силами притяжения и отталкивания можно пренебречь.

В природе такого газа не существует, но близкими по свойствам можно считать реальные разреженные газы, давление в которых превышает на 200 атм и находящихся по не очень низкой температуры.

2. Пусть газ находится в закрытом сосуде. Манометр показывает давление газа р0. Но какова природа этого давления? Каждая из молекул газа, ударяясь о стенку, в течение малого промежутка времени действует на нее с определенной силой. Вследствие беспорядочных ударов об стенку, сила, действующая со стороны всех молекул на единицу площади стенки,- это давление. Действия, вызванные ударом отдельных молекул, настолько малы, что манометр их не регистрирует. Манометр фиксирует среднюю по времени силу, действующую на каждый квадратный сантиметр его чувствительного элемента - мембраны. Среднее значение давления р0 - практически вполне определенная величина, ибо ударов об стенку очень много, а массы молекул чрезвычайно малы.

3. Пусть внутри сосуда, площадь стенки которой S, содержится идеальный одноатомный газ, масса каждой молекулы m0, они хаотично движутся со скоростями .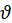

Общее число молекул в сосуде N, а через 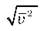обозначим среднюю квадратичную скорость их движения:

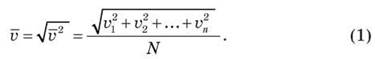
Эксперимент свидетельствует, что в случае неизменной температуры сосуда и газа, скорость молекул газа также является постоянной и определяется по формуле (1).

Квадрат вектора скорости связан с его компонентами следующим соотношением:

Полная хаотичность движения позволяет утверждать, что движение по всем направлениям происходит с одинаковой скоростью, поэтому

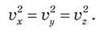
Поэтому формула 2 будет иметь вид:

Предположим, что молекулы газа движутся от одной грани к другой без столкновений.

Это упрощение вследствие большого количества молекул N и хаотичности их движения не влияет на точность расчетов. Во время столкновения со стенками сосуда молекулы идеального газа взаимодействуют с ними по законам механики как абсолютно упругие тела. Молекула действует на стенку с силой F2, равная, согласно третьему закону Ньютона, силе F1, с которой стенка сосуда действует на молекулу и противоположная ей по направлению.

Пусть молекула массой т0 движется в направлении стенки сосуда, площадь которой S.

Упруго ударившись о стенку, она передает ей импульс:

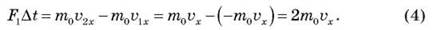
За время Δt стенки сосуда могут достичь лишь те молекулы, которые содержатся в объеме:

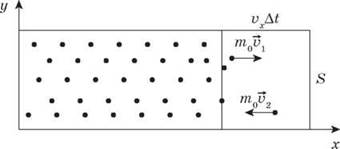
Поскольку в этом объеме половина молекул движется к стенке, а половина от нее, то количество молекул Z, которые ударятся о стенку за время Δt, равна:

где 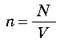- концентрация молекул, [n] = м-3. Подставив значения объема V из уравнения (5) в уравнение (6) получим:

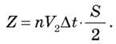
Все эти молекулы передают стенке сосуда импульс, что, согласно второму закону Ньютона, равно импульсу силы:

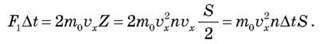
После упрощения сила F, с которой молекулы действуют на стенку S, равна:

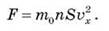
Так 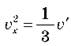, а давление 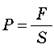, то получим выражение основного уравнения МКТ газов:

Учтем то, что квадрат модуля скорости движения молекул равна среднему значению квадрата скорости 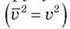, поэтому уравнение (7) будет иметь вид:

Это и есть основное уравнение МКТ.

Давление молекул на стенки сосуда равна 1/3 произведению концентрации молекул на массу одной молекулы и на средний квадрат скорости движения молекул.

Основное уравнение МКТ связывает макроскопические величины - давление, которое можно измерить манометром, с микроскопическими величинами, характеризующими молекулы, и является как бы мостом между двумя мирами - макроскопическим и микроскопическим.

Если через 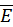0 обозначим среднюю кинетическую энергию поступательного движения молекул

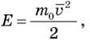
то уравнение (8) примет следующий вид:

давление молекул идеального газа пропорционален произведению числа молекул в единице объема на среднюю кинетическую энергию поступательного движения молекул.

Так 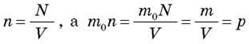, уравнение (8) примет следующий вид:

где ρ - плотность газа.

III. Закрепление изученного материала

Задача. Плотность газа в баллоне газопаливної электрической лампочки ρ = 0,9 кг/м3. Когда лампочка светится, давление газа возрастает с р1 = 8·104 Па до р2 = 1,1·105 Па. На сколько увеличилась при этом средняя скорость молекул газа?

Дано: р = 0,9 кг/м3, р1 = 8·104 Па, р2 = 1,1·105 Па.

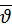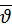Найти: 2 - 1 - ?

Решение

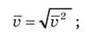
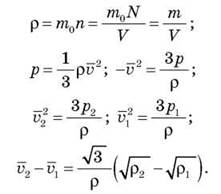
IV. Домашнее задание

Выучить конспект.

Задача. Под каким давлением находится газ в сосуде, если средний квадрат скорости его молекул 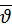2 = 106 м2/c2. Концентрация молекул n = 3·1025 м-3, масса каждой молекулы m0 = 5·10-26 кг.