ГЕОМЕТРИЯ

Раздел ІІ. СТЕРЕОМЕТРИЯ

КОНТРОЛЬНЫЙ ТЕСТ № 1.

1. Какие из приведенных утверждений правильные?

I. Любые две точки всегда принадлежат одной прямой.

II. Любые три точки всегда принадлежат одной прямой.

III. Любые три точки всегда принадлежат одной плоскости.

2. Прямые АВ и СD пересекаются. Укажите все возможные случаи взаимного расположения прямых АС и ВD.

3. Сколько различных плоскостей можно провести через две скрещивающиеся прямые.

4. Через конец М отрезка МN проведена плоскость β. Через конец N и точку В этом отрезка проведены параллельные прямые, пересекающие плоскость β в точках N₁ и₁ соответственно. Найти отношение МВ₁ : МN₁, если МВ : ВN =3 : 2.

5. АВСD - трапеция, периметр которой равен 20 см. Точка М не лежит в плоскости трапеции. Найти периметр четырехугольника А₁В₁С₁D₁, где А₁, В₁, С₁, D₁ - середины отрезков МА, МВ, МС, МD.

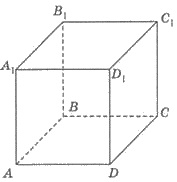
6. АВСDА₁B₁C₁D₁ - прямоугольный параллелепипед (рисунок). Какая из предложенных плоскостей параллельна к плоскости АА₁B₁?

7. Прямая m пересекает плоскость α, а прямая n параллельна плоскости α. Укажите все возможные случаи размещение прямых m и n.

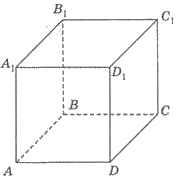
8. АВСDА₁В₁С₁D₁ - куб (рисунок). Которая с предложенных прямых параллельна плоскости АА₁С₁?

9. Какая из предложенных фигур не может быть параллельно проекцией параллелограмма?

10. Треугольник АВС является изображением треугольника А₀В₀С₀; ВК - изображение биссектрисы В₀К₀ треугольника А₀В₀С₀; А₀В₀ = 6 см; В₀С₀ = 9см; А₀С₀ = 10 см. Найти отношение АК : КС.

11. Параллелограмм ABCD и трапеция ABKL, в которой АВ || KL, не лежат в одной плоскости; М - середина ВК; N - середина AL. Найти (в см) MN, если CD = 8 см; LK = 6 см.

12. Два лучи с началом в точке А пересекают одну из параллельных плоскостей в точках K₁ и L₁, а другую в точках К₂ и L₂ соответственно; K₂L₂ = 30 см; АК₁ : АК₂ = 4 : 5. Найти (в см) длину отрезка K₁L₁.