ГЕОМЕТРИЯ

Раздел И. ПЛАНИМЕТРИЯ

§5. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ПРИЗНАКИ И СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ.

3. Признаки параллельности прямых.

Признак (в геометрии) - это теорема, которая утверждает, что при выполнении определенных условий можно установить параллельность прямых, равенство фигур, принадлежность фигуры к определенному классу и т.д.

Признак параллельности прямых. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

На рисунке 165: с - секущая для а и b. Если 1 = 5 или 2 = 6 или 3 = 7 или 4 = 8, то а || b.

Следствие 1. Если при пересечении двух прямых секущей внутренние разносторонние углы равны, то прямые параллельны.

На рисунке 165: с - секущая для а и b. Если 3 = 5 или 4 = 6, то а || b.

Следствие 2. Если при пересечении двух прямых секущей сумма внутренних односторонних углов равна 100°, то прямые параллельные.

На рисунке 165: с - секущая для а и b. Если 4 + 5 = 180° или 3 + 6 = 180°, то а ll b.

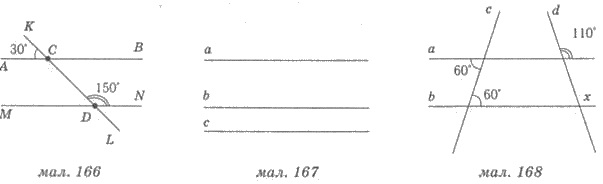
Пример. Являются ли параллельными прямые АВ и MN на рисунке 166?

Решения. BCD = ACK (как вертикальные), BCD = 30°. Поскольку 30° + 150° = 180°, тo сумма внутренних односторонних углов BCD и CDN равна 180°. Поэтому, за следствием 2, АВ || MN.