Наибольший общий делитель (нод)

Наибольшее натуральное число, на которое делится каждое из чисел a и bназывается наибольшим общим делителем чисел a и b и обозначается НОД (a; b). НОД можно искать для любого количества чисел. Для нахождения наибольшего общего делителя нескольких натуральных чисел, надо разложить эти числа на простые множители и найти произведение общих множителей. Например:
; ;
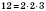
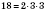
НСД .
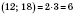
Если разложение на простые множители записанное с использованием степеней, надо найти произведение степеней с одинаковыми основаниями с показателями, которые являются наименьшими из использованных для записи чисел. Например:
; ;
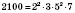
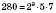
НСД .
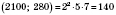
Если все данные числа кратные одному из них, это число будет наибольшим общим делителем данных чисел. Например:
НСД .
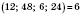
Два натуральных числа, наибольший общий делитель которых равен 1, называются взаимно простыми. Два простых числа всегда будут взаимно простыми (например, 13 и 23). Степени различных простых чисел также являются взаимно простыми. Например:
; ;
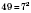
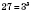
НСД .
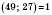