1-й семестр

МЕХАНИКА

2. Динамика

Урок 12/32

Тема. Сила упругости. Закон Гука

Цель урока: ознакомить учащихся с природой силы упругости, зависимости силы упругости от деформации

Тип урока: изучение нового материала

План урока

ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА

1. Природа силы упругости

Вследствие каких-либо деформаций тела всегда возникают силы, препятствующие деформациям; эти силы направлены в сторону восстановления прежних форм и размеров тела, т.е. направлены противоположно деформації. их называют силами упругости.

Ø Сила упругости - это сила, возникающая в результате деформации тела и направленная противоположно направлению смещения частиц в процессе деформации.

Любое тело состоит из частиц (атомов или молекул), а те, в свою очередь, состоят из положительного ядра и отрицательных электронов. Между заряженными частицами существуют силы электромагнитного притяжения и отталкивания. Если частицы находятся в состоянии равновесия, то силы притяжения и отталкивания урвновешивают друг друга.

В случае деформации тела происходят изменения во взаимном расположении частиц. Если расстояние между частицами увеличивается, то электромагнитные силы притяжения превышают силы отталкивания. Если же частицы сближаются, то преобладают силы отталкивания.

Силы, возникающие в результате изменения расположения частиц очень малы. Но вследствие деформации изменяется расположение очень большого количества частиц, поэтому равнодействующая всех сил уже является значительной. Это и есть сила упругости. Следовательно, сила упругости по своему происхождению - электромагнитная сила.

2. Механическое напряжение

Состояние упруго деформированного тела характеризуют физической величиной, называется механическим напряжением.

Будем растягивать с определенной силой металлический стержень. В любом сечении S деформированного стержня возникают силы упругости, которые препятствуют его разрыву.

Ø Механическое напряжение σ - это физическая величина, которая характеризует деформированное тело и равен отношению модуля силы упругости Fnp к площади поперечного сечения тела S:

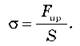
Единица механического напряжения в СИ - паскаль (Па).

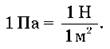
Опыты показывают, что:

Ø в случае незначительных упругих деформаций механическое напряжение пропорционально относительному удлинению:

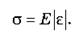
Коэффициент пропорциональности Е называется модулем упругости, или модулем Юнга.

Ø Модуль Юнга - это физическая величина, которая характеризует сопротивляемость материала упругой деформации растяжения или сжатия.

Поскольку относительное удлинение ε - безразмерная величина, то единица модуля Юнга в СИ - паскаль (Па).

3. Закон Гука

В 8 классе мы изучали закон Гука:

Ø в пределах упругой деформации сила упругости прямо пропорциональна абсолютному удлинению пружины: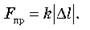

Жесткость пружины определяется по формуле:

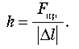
Отсюда следует, что единица жесткости в системе СИ измеряется в Н/м.

Покажем, что выражение 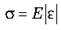также является законом Гука, но в другой форме записи.

По определению, 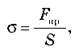а относительное удлинение 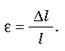Тогда с учетом формулы 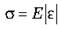получаем:

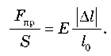
Отсюда:

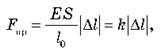
где 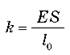- коэффициент жесткости. Следовательно,

Ø коэффициент жесткости зависит от упругих свойств материала, из которого изготовлено тело, и его геометрических размеров.

Прямую пропорциональную зависимость между силой упругости и удлинением используют в динамометрах. Сила упругости часто работает в технике и природе: в часовых механизмах, в амортизаторах на транспорте, в канатах, тросах, в человеческих костях и мышцах т.д.

Вопрос к ученикам во время изложения нового материала

1. Когда возникает сила упругости?

2. Почему возникает сила упругости и как она направлена?

3. Что характеризует механическое напряжение?

4. От чего зависит коэффициент жесткости?

ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА

1). Тренируемся решать задачи

1. Чтобы растянуть пружину на 2 см, нужно приложить силу в 10 Н. Какую силу нужно приложить, чтобы растянуть пружину на 6 см? на 10 см?

2. Вычислите массу груза, висящего на пружине жесткостью 100 Н/м, если удлинение пружины равно 1 см?

3. Вследствие сжатия буферной пружины на 3 см возникает сила упругости 6 кН. На сколько вырастет эта сила, если сжать пружину еще на 2 см?

4. С вертолета, зависшего на определенной высоте над поверхностью Земли, опускают стальной трос. Какой может быть длина троса, чтобы он не оборвался под собственным весом? Максимальное механическое напряжение, которое может выдержать сталь, составляет 320 МПа.

Решение

Из условия задачи следует, что сила тяжести, которая действует на трос, равна силе упругости:

Fт = Fпр.

Вычислим силу притяжения с учетом того, что m = ρV и V = Sl:

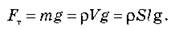
Для вычисления силы упругости воспользуемся определением механического напряжения: 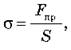откуда получаем:

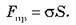
Следовательно,

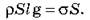
Окончательно получаем:

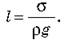
Проверяем единицы величин:

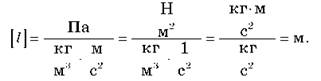
Подставляя числовые величины, получаем, что длина троса равна 4 100 м.

(Ответ: 4,1 км).

2). Контрольные вопросы

1. От чего зависит модуль силы упругости?

2. Очертите границы применимости закона Гука.

3. Что характеризует модуль Юнга?

Что мы узнали на уроке

• Сила упругости - это сила, возникающая в результате деформации тела и направленная противоположно направлению смещения частиц в процессе деформации.

• Механическое напряжение σ - это физическая величина, которая характеризует деформированное тело и равен отношению модуля силы упругости Fnp к площади поперечного сечения тела S:

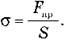
• В случае небольших упругих деформациях механическое напряжение пропорционально относительному удлинению:

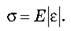
• Модуль Юнга - это физическая величина, которая характеризует сопротивляемость материала упругой деформации растяжения или сжатия.

• Коэффициент жесткости зависит от упругих свойств материала, из которого изготовлено тело, и его геометрических размеров.

Домашнее задание

1. П.: § 26.

2. 36.:

г1) - 9.3; 9.6; 9.7; 9.8;

р2) - 9.13; 9.14; 9.15; 9.16;

г3) - 9.40; 9.42; 9.43; 9.44.