МАТЕМАТИКА

ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ

Первоначальная функция

Первоначальной для данной функции y = f(x) на промежутке (а; b) называется такая функция F(x), производная которой для всех х 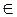(а;b), равна f(x): F'(x) = f(x).

Общий вид первообразной F(x) + C, где С - произвольное постоянное число.

Теорема.

Любая непрерывная на [а; b] функция y = f(x) имеет первоначальную функцию.

Определенный интеграл: 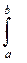f(x)dx.

Формула Ньютона-Лейбница:

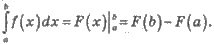
Применение определенного интеграла:

1. Вычисление площадей плоских фигур

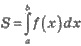
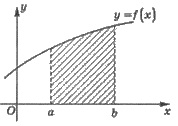
2. Вычисление объемов тел

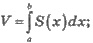
S(x) - площадь сечения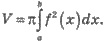

3. Вычисление расстояния по известным законом изменения скорости:

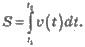
4. Вычисление работы переменной силы: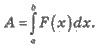

5. Вычисления количества электричества: