МЕХАНИКА

3. ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ

3.5. ВИДЫ МЕХАНИЧЕСКОЙ ЭНЕРГИИ И ИХ СВЯЗЬ С РАБОТОЙ

Кинетическая и потенциальная энергия составляют механическую энергию. Она характеризует механическое движение.

Кинетическая энергия - это энергия движущегося тела.

Кинетическая энергия в классической механике:

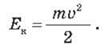
Поскольку скорость тела является величиной относительна, т.е. зависит от выбора системы отсчета, то и кинетическая энергия относительная. Кинетическая энергия всегда положительная.

Кинетическая энергия в релятивистской механике:

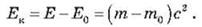
Потенциальная энергия - это энергия, обусловлена взаимодействием тел или частиц тела.

В механике различают:

а) потенциальную энергию тела, поднятого над Землей:

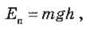
где h - высота над уровнем, на котором потенциальная энергия системы «Земля - тело» принимается за ноль (нулевой уровень потенциальной энергии);

б) потенциальную энергию упруго деформированного тела:

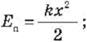
в) потенциальную энергию гравитационного взаимодействия двух материальных точек с массами m₁ и m₂, находящихся на расстоянии r друг от друга:

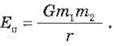
Потенциальная энергия положительная, если она обусловлена силами отталкивания, и отрицательная, если обусловлена силами притяжения.

Закон сохранения механической энергии: полная механическая энергия системы тел, в которой действуют только консервативные силы (потенциальные), является величиной постоянной.

Консервативные силы - это силы тяготения, упругости, кулоновские силы.

Консервативная сила - сила, работа которой при перемещении тела зависит только от начального и конечного положений тела в пространстве. Например, работа силы тяжести (рис. 46):

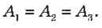
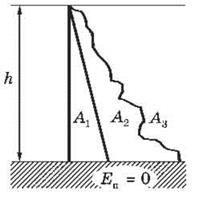
Рис. 46

Работа консервативных сил в любом замкнутом контуре равна нулю (рис. 47).

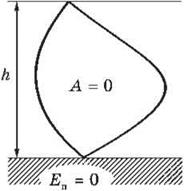
Рис. 47

Потенциальный поле - поле консервативных сил.

Кинетическая и потенциальная энергия - функции состояния системы, то есть могут быть точно определенным, если известны координаты и скорости всех тел системы, а также система отсчета.