ФИЗИЧЕСКИЙ ПРАКТИКУМ*
Практическая работа № 5
Тема. Определение модуля упругости резины
Цель: экспериментально проверить закон Гука и определить модуль упругости резины.
Приборы и материалы: резиновая полоска длиной 20-30 см; набор гирь по 102 г; измерительная линейка с ценой деления 5 мм/под; штатив универсальный с муфтой и лапкой; штангенциркуль.
Теоретические сведения
При деформации тела возникает сила упругости. При малых деформациях сила упругости создает механическое напряжение σ, прямо пропорциональна относительной деформации ε. Эта зависимость называется законом Гука и имеет такой вид:
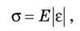
где σ = F/S; F - сила упругости; S - площадь поперечного сечения образца;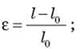 
l - l0 - абсолютная деформация; l0 - начальная длина образца; l - длина растянутого образца; Е = σ/ε-модуль упругости (Юнга). Он характеризует способность материала противостоять деформации и численно равен механическому напряжению при ε = 1 (т.е. когда l = 2l0). Реально такой деформации не выдерживает ни одно твердое тело и разрушается. Уже за значительной деформации она перестает быть упругой и закон Гука не выполняется. Чем больше модуль Юнга, тем меньше деформируется стержень при прочих равных условиях (одинаковых F, S, l0).
ХОД РАБОТЫ
1. Штангенциркулем измерьте диаметр D резиновой полоски и вычислите ее площадь поперечного сечения по формуле:
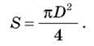
2. Закрепите свободный конец резиновой полоски в штативе и измерьте с помощью линейки ее начальную длину l0 от нижнего края лапки штатива до места крепления тягарця.
3. Подвешивая к нижней петли по очереди грузики (рис. 1), измеряйте каждый раз новую длину резиновой полоски l. Вычислите абсолютное удлинение полоски: l - l0.
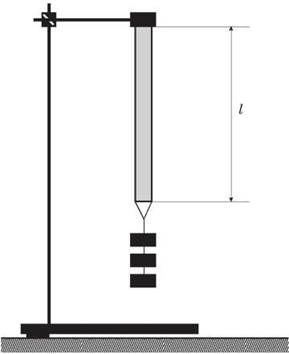
Рис. 1
4. Определите приложенную силу F = mg, где g = 9,8 м/c2. Результаты запишите в таблицу.
№ опыта |
F, H |
l, м |
l - l0, м |
σ, Па |
ε |
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
5 |
|
|
|
|
|
5. По полученным данным постройте график зависимости механического напряжения σ от относительного удлинения ε.
6. Выделите на графике прямолинейную участок и в ее пределах вычислите модуль упругости по формуле:
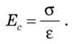
7. Вычислите относительную и абсолютную погрешности измерений модуля Юнга для одной из точек, что принадлежит прямолинейном участке графика, по формулам:
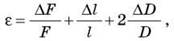
где ΔF = 0,05 Н, Δl = 1,5 мм, ΔD = 0,1 мм; ΔE = Eε.
8. Запишите результат в виде:
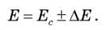
9. Сделайте вывод о проделанной работе.
Контрольные вопросы
1. Почему модуль Юнга выражается таким большим числом?
2. Почему практически невозможно определить модуль Юнга прямыми измерениями по определению?