АЛГЕБРА И НАЧАЛА АНАЛИЗА
Раздел III. ФУНКЦИЯ
§5. ФУНКЦИИ у = k/x; y = x2; у = √x, ИХ ГРАФИКИ И СВОЙСТВА.
1. Функция у = k/x, ее график
Обратной пропорциональностью называют
функцию, которую можно задать формулой вида у = k/x, где х - независимая переменная, k - некоторое число, отличное от нуля.
Областью допустимых значений функции в
= k/x является множество всех действительных чисел, кроме нуля. Графиком функции у = k/x является гипербола, причем, если k > 0, то ее ветви расположены в i И III
координатных четвертях, а если k 0, то во II и IV координатных
четвертях.
Пример 1. Построить график функции y = 6/x.
Решения. Составим таблицу
значений функции у = 6/x для нескольких значений аргумента.
|
x
|
-6
|
-3
|
-2
|
-1
|
1
|
2
|
3
|
6
|
|
y
|
-1
|
-2
|
-3
|
-6
|
6
|
3
|
2
|
1
|
Обозначим эти точки на координатной
плоскости и соединим плавными линиями точки каждой из ветвей гиперболы (рис. 69).
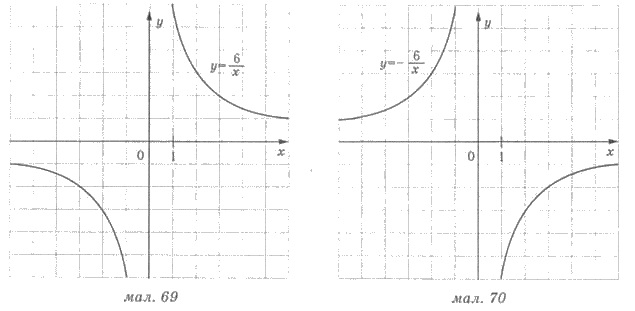
Пример 2. Построим график функции у = -6/x.
Решения. Составим таблицу
значений функции у = -6/x для нескольких
значений аргумента.
|
x
|
-6
|
-3
|
-2
|
-1
|
1
|
2
|
3
|
6
|
|
y
|
1
|
2
|
3
|
6
|
-6
|
-3
|
-2
|
-1
|
График функции изображен на рисунке
70.