Математика - Алгебра

Натуральные числа и действия над ними

Действия над натуральными числами

Добавление

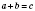
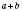
В записи числа a и b - слагаемые, число с, а также выражение - сумма чисел а и b.
Свойства сложения
1. Переставная. От перестановки слагаемых сумма не меняется: .
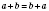
2. Связующее. Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел .
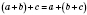
Переставная и соединительная свойства сложения дают возможность выполнять сложение нескольких чисел в любой последовательности:
.
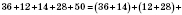
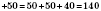
3. Если один из двух слагаемых 0, то их сумма равна второму слагаемому:
; .

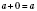
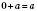
Вычитание

Действие, с помощью которого по известной сумме двух слагаемых и одному из них находят второе слагаемое, называетсядействием вычитания: .
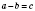
В этой записи число а - уменьшающееся, b - вычитаемое, c - разница.
Разность двух натуральных чисел показывает, на сколько первое число больше второго или на сколько второе число меньше первого.
Свойства вычитания
1. Чтобы вычесть сумму от числа, можно сначала вычесть из этого числа одно слагаемое, а потом из полученной разности - второе:
.
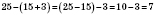
2. Чтобы от суммы вычесть число, можно вычесть его от одного из слагаемых, а к полученной разности прибавить второе слагаемое:
;
.
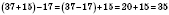
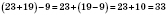
3. Если из числа вычесть нуль, оно не изменится: .
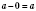
4. Если из числа вычесть то же самое число, получим 0: .

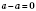
Умножения

Умножить число a на число b - значит найти сумму b слагаемых, каждый из которых равен а:
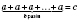
или ,
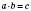
где a и b - множители, c - произведение.
Свойства умножения
1. Переставная.От перестановки множителей произведение не меняется:
.
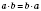
2. Связующее.Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел:
.
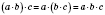
Соединительная и переставная свойства умножения распространяются на произвольное количество множителей и позволяют выполнять умножение в произвольном порядке: .
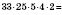
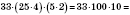
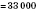
3. Распределительная.
Чтобы умножить сумму на число, можно каждое слагаемое умножить на это число и найденные произведения добавить:
.
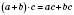
Чтобы умножить разность на число, можно уменьшающееся и вычитаемое умножить на это число и от первого произведения вычесть второе:
.
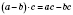
4. Если единицу умножить на любое число, получим то же число:
.
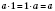
5. Если хотя бы один множитель равен 0, произведение равно 0:
.
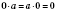
Примеры

;
.

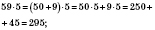
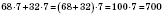
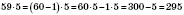
Деления

Деление - действие, с помощью которого по известным произведением и одним из множителей находится второй множитель.
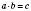
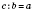
Если , то и .
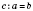
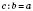
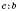
В записи число с - делимое, b - делитель, число а, а также выражение - доля.
Доля показывает, во сколько раз делимое больше делителя.
Свойства деления
1. На 0 делить нельзя.
2. Если разделить число на 1, получим то же число: .
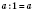
3. Если разделить число на себя, получим 1: .
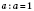
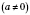
4. Если разделить 0 на любое число, кроме 0, получим 0: .
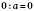
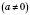
Деление с остачею
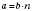
Число а делится на число b нацело, если , где n - какое-нибудь натуральное число.
Например, 15 делится нацело на 3, поскольку .
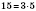
В противном случае можно разделить а на b с остачею. Например:
.
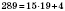
В этой записи число 289 - делимое, 15 - делитель, 19 - неполная доля, 4 - остаток.
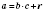
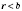
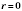
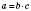
Для любых чисел а и b всегда найдутся такие числа с и r (натуральные или 0), что , где . Если , то , т.е. число а делится как на число b, так и на число c.

Назад

Содержание

Вперед