Часть 1 МЕХАНИКА

Глава 2 ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ

2.8. Неінерційні системы отсчета

Опыт показывает, что законы Ньютона сбываются только в инерциальных системах отсчета. Любая система неінерційна движется относительно инерциальных систем с некоторым ускорением. В неинерционных системах отсчета законы Ньютона не оправдываются. Рассмотрим это на примерах.

Пусть на гладкой платформе без бортов (рис. 2.3) лежит тело А. Когда платформу сдвинуть с места, то тело сдвинется. Как можно объяснить это явление? С точки зрения наблюдателя, который находится в инерционной системе, связанной с Землей (в этом случае пренебрежем ее неінерційністю), равнодействующая сила, приложенная к телу А, равна нулю, поэтому ускорение его равно нулю. Платформу потащили вперед, она получила ускорение 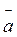₀, а А тело осталось на прежнем месте.

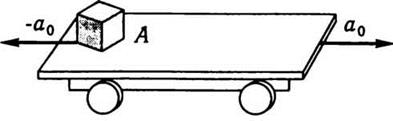
Рис. 2.3.

С точки зрения наблюдателя, который находится в ускоренной системе отсчета, связанной с платформой, это явление можно объяснить так: тело А сдвинулся назад, получив ускорение. При этом сила, действующая на тело, равна нулю, а ускорение - отличное от нуля.

Итак, для ускоренной системы закон инерции и второй закон динамики не выполняются. Такую систему называют неінерційною.

Аналогичный пример можно рассмотреть с вагоном, который получает ускорение 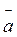₁, и мячом А, что лежит на гладкой полочке и начнет двигаться с ускорением 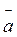₁. С точки зрения пассажира в вагоне (то есть ускоренной системы) мяч приобрел ускорение, хоть на него сила не действовала. Итак, тело в ускоренной системе отсчета будет в покое только во время действия на него внешних сил.

В механике часто учитывают движение ускоренной системы введением особых сил, так называемых сил инерции. Введение этих сил дает возможность сохранить для тел, движущихся относительно неинерционных систем, первый и второй законы динамики в той самой форме, которую они имеют для тел, движущихся относительно инерциальных систем отсчета. Это существенно упрощает анализ движения в каждом отдельном случае.

В первом случае будем считать, что к тела А приложено некоторую силу 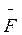_и. По второму закону Ньютона

где m - масса тела; 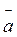₀ - ускорение платформы относительно Земли.

Во втором случае сила инерции, действующая на мяч,

где m - масса мяча; 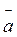₁ - ускорение вагона.

Величина 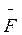_и имеет размерность силы, однако этого не достаточно, чтобы считать ее силой. Ведь разные физические величины могут иметь ту же размерность (например, работа и момент силы). Сила есть механическим воздействием одного тела на другое. При этом всегда должна быть соответствующая сила «противодействия». Сила - причина «истинного» ускорение, ускорение относительно инерциальной системы отсчета. Сила инерции приложена к телу, но она не является результатом непосредственного действия второго тела, ибо такого тела просто нет. Поэтому для силы инерции нет и противодействия. Она не проявляется также на «истинном» ускорении.

Представим себе, что на платформе лежит несколько тел, которые отличаются массами. В формуле (2.15) для разных тел масса m неодинакова для каждого тела, а множитель а₀ - то же для всех тел. Это свидетельствует о том, что силы инерции, которые действуют на тела системы, возникают в результате ускорения системы отсчета (платформы), а не в результате взаимодействия тел между собой. Силы инерции увеличиваются с увеличением ускорения системы отсчета и равны нулю, если система отсчета движется равномерно и прямолинейно.

Итак, за наличием и значением сил инерции можно делать вывод о степени неінерційності системы. Силы инерции нельзя сравнивать с такими силами, как упругие, трения, то есть силами, что обусловленные действием на тело других сил. Силы инерции обусловлены свойствами той системы отсчета, в которой рассматриваются механические явления.

Изучение сил инерции не является принципиально необходимым. Любое движение всегда можно рассмотреть относительно инерциальной системы отсчета. Однако практически очень часто интересен именно движение относительно неинерционных систем отсчета. Использование сил инерции дает возможность решить соответствующую задачу непосредственно в такой системе отсчета, что гораздо проще, чем рассматривать движение в инерционной системе.

Следовательно, введение сил инерции дает возможность описывать движение тел в любых (как инерциальных, так и неинерционных) системах отсчета с помощью одних и тех же уравнений движения.