Часть 5 АТОМНАЯ ФИЗИКА

Раздел 15 СТРОЕНИЕ АТОМА

15.3. Лінійчасті спектры

Строение спектров атомов также противоречит законам классической физики. Исходя из классической электродинамики, электрон, двигаясь по орбите, должен равномерно излучать энергию, а потому атомный спектр должен быть сплошным. На самом деле спектр паров и газов, то есть практически изолированных атомов, лінійчастий. Частоты линий в спектре связаны со строением химических элементов. Спектры поглощения и излучения вещества взаємооборотні. Спектр каждого элемента в газообразном состоянии состоит из комплексов линий, что закономерно связаны между собой. Комплекс линий, подлежат определенному закону, называют спектральной серией. Расстояние между линиями уменьшается при увеличении частоты (рис. 15.3).

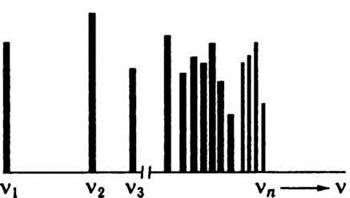
Рис. 15.3

В спектроскопии для характеристики спектральных линий вводят величину, получившую название волнового числа. Волновое число ν' равно количеству длин волн, что умещается в 1 см. Следовательно,

Использование для характеристики спектральных линий волнового числа ν вместо частоты ν’ связано с тем, что современные экспериментальные методы позволяют измерить длину волны (а следовательно, и волновое число) с гораздо большей точностью, чем точность определения скорости света. Поэтому значение частоты не может быть столь же точным, как значение волнового числа.

Лінійчасті спектры различных элементов отличаются друг от друга. В большинстве металлов количество линий в этих спектрах очень большая (в железе, например, более 5000 линий), а сами линии имеют разную интенсивность.

Рассмотрим спектр простейшего атома - атома водорода. В видимой части его наибольшую интенсивность имеют три линии: красная, сине-зеленая и фиолетовая; их принято обозначать символами Н_α, H_β, H_γ. Наряду с ними в видимой части спектра есть и другие линии меньшей интенсивности. Есть также немало линий в ультрафиолетовой и инфракрасной областях спектра.

В 1885 г. швейцарский физик И. Бальмер установил, что длины волн девяти известных на то время линий в спектре водорода (эти линии располагаются в видимой части спектра) можно определить по

где λ₀ - постоянная величина, равная 364,613 нм, а λ для различных линий серии приобретает последовательно значений целого ряда чисел, начиная с трех, то есть n = 3, 4, 5, 6,...________

Соотношение (15.6) часто записывают для волнового числа

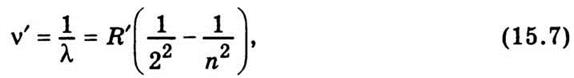
Где R’ = 10 973 731,53 м^-1 - постоянная Ридберга; n = 3, 4, 5,... Если n = С, то ν' точно совпадает с волновым числом красной гідрогенової линии Н_α, при n = 4 имеем волновое число зеленой линии Н_β и при n = 5 - волновое число фиолетовой линии Н_γ. Другие значения n точно определяют волновые числа около 30 линий, спектроскопічно выявленных в видимой и близкой ультрафиолетовой части спектра водорода, которые образуют так называемую серию Бальмера. С увеличением n дробь 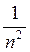уменьшается и соответственно формулы (15.7) уменьшается также разность волновых чисел двух соседних линий. При достаточно больших n линии чрезвычайно тесно размещаются друг возле друга. На рис. 15.4 схематически показано это постепенное сгущение линий в спектре водорода, приближение их к грани, которая достигается при неограниченном росте n.

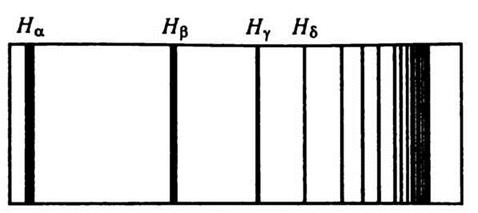
Рис. 15.4

И. Рідберг показал, что в лінійчастих спектрах не только водорода, но и других элементов наблюдаются спектральные серии, причем частоты ν всех линий этой серии удовлетворяют условие

где l i n - целые числа. Функции Т(i) и Т (n) называют спектральными термами. В рамках этой серии l является постоянной величиной, а n изменяется.

В 1908 г. В. Ритц установил справедливость положения, которое называют комбинационным принципом Ридберга - Ритца: частоты спектральных линий излучения любого атома можно представить как разность двух термов. Осуществляя различные комбинации термов, можно найти все возможные частоты спектральных линий определенного атома. Исходя из комбинационного принципа Ритца, следует ожидать, что в спектре водорода кроме серии Бальмера есть и другие серии. Последующие исследования доказали справедливость этого выводу. Частоты всех линий в спектре атома водорода можно определить по обобщенной формулой Бальмера:

где R = R'c = 3,28984 ∙ 10¹⁵ с^-1 также называют постоянной Ридберга; l и n - целые числа, причем n ≥ l + 1.

Значение l = 1 и n = 2,3,4,... соответствуют серии Лаймана, которое найдено в далекой ультрафиолетовой области спектра; при l=2 и n = 3, 4, 5,... получим серию Бальмера; l = 3, n = 4, 5, 6,... определяют серию Пашена в инфракрасной участке спектра. В далекой инфракрасной области найдено серию Брекета (l = 4, n = 5, 6,...), серия Пфунда (l = 5, n = 6, 7,...) и серию Хэмфри (l = 6, n = 7, 8, ...).

Все приведенные формулы эмпирические - это правила, с помощью которых можно определить частоты спектральных линий для атома водорода. Однако с самого начала было понятно, что эти правила имеют глубокий физический смысл. Были сделаны попытки объяснить строение лінійчастих спектров по помощью классической теории внутриатомных вибраторов. Теорию внутриатомным вибраторов разработали X. Лоренц, П. Друде и др. Они выходили из представления, что внутри атома оптически активные электроны под действием электромагнитных волн света приходят в гармоничное колебательное движение относительно некоторых центров равновесия. На основе этой модели было объяснено экспериментально установлены законы поглощения и дисперсии света. Считали, что теория внутриатомным вибраторов, совмещенная с ядерной моделью атома, также объяснит происхождение лінійчастих спектров. Однако проведенные расчеты доказали невозможность даже приближенно решить эту задачу таким способом.

Как уже упоминалось, из основных законов классической электродинамики следует, что электрон, двигаясь по орбите, должен непрерывно излучать энергию и при уменьшении своей энергии приближаться к ядру. Следовательно, частота вращения ν₀ и частота излучающего света должны постепенно варьироваться.

Таким образом, если бы классическая электродинамика, нашла свое подтверждение в многочисленных опытах в сфере макрофізичних процессов, была бы справедливой и для внутриатомных процессов, то спектр излучения атома состоял бы из серий линий с частотами, кратными частоте вращения электрона вокруг ядра (чего нет на самом деле). Совокупность большого числа атомов одного элемента излучала бы сплошной спектр (тогда как излучается лінійчастий спектр). Вследствие непрерывных потерь энергии на излучения и вызванное этим приближения внутриатомных электронов к ядра, все атомы были бы нестабильными. На самом деле атомам присуща исключительная стабильность и спектры, характеризующие их структуру, остаются неизменными даже при столкновении атомов.