Часть 4

ОПТИКА. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ

Раздел 12 ВОЛНОВЫЕ СВОЙСТВА СВЕТА

12.4. Дифракция света

Геометрическая оптика основывается на принципе прямолинейности распространения света в однородной среде, где нет преломления, отражения или других аналогичных явлений. Кроме того, считалось, что световой пучок можно разбить на любое количество бесконечно тонких лучей и наблюдать распространение каждого из них отдельно.

При наблюдении интерференции пользуются также представлениями о бесконечно тонкие световые лучи, которые прямолинейно распространяются в однородной среде. Уточнения по сравнению с геометрической оптикой заключалось лишь в том, что эти лучи рассматриваются как направления распространения световых колебаний. Немало фактов свидетельствует, что требуется дальнейшее уточнение представлений о процессе распространения световых колебаний. Необходимость в таком уточнении возникает сразу при первой попытке достать на опыте достаточно узкий световой луч.

Проще всего достать узкий световой луч, если взять достаточно малое источник света S и поместить на некотором расстоянии от него непрозрачный экран К с небольшим отверстием. Диаметр светящейся пятна аb, который образуется на экране N, размещенном за экраном K, будет характеризовать ширину создаваемого светового пучка (рис. 12.10).

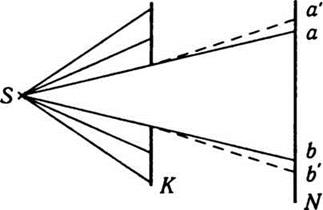
Рис. 12.10

Следовательно, с геометрической оптики следует: чем меньше будет отверстие в экране К, тем меньше будет диаметр светящейся пятна на экране N или тем более узким будет световой луч. Если отверстие в экране уменьшить вплоть до ничтожно малого, то казалось бы, что можно получить как угодно узкий световой луч, который бы создал на экране светящуюся точку. Однако опыт дает совершенно противоположный результат: начиная с определенного размера отверстия, дальнейшее его уменьшение вызывает не уменьшение светящейся пятна на экране N, а ее увеличение. При этом пятно теряет свою резкость, становится расплывчатым и освещенной неравномерно, на ней возникает немало колец (для круглого отверстия) в участке а'b’ значительно более широкой, чем это следует из геометрической оптики. Расширение пятна соответствует, конечно, и расширению светового луча. Итак, попытка достать как угодно узкий луч света потерпела неудачу. Описанное явление обусловлено дифракцией света.

В общих чертах явление дифракции заключается в том, что при прохождении через очень узкие отверстия и около краев непрозрачных экранов свет заметно отклоняться от прямолинейного распространения. В участке геометрической тени и вблизи нее в освещенной части поля зрения наблюдаются попеременные ослабление освещенности такого же характера, как и при интерференции когерентных световых пучков. Это позволяет прийти к выводу, что основой явлений дифракции и интерференции является волновая природа света.

Сторонники корпускулярной теории света пытались объяснить искривление световых лучей тем, что частицы света притягиваются краями экрана. Тогда отклонения лучей должно зависеть от формы краев проема и материала экрана. О. Френель доказал, что это не так. Интересно отметить, что один из основоположников волновой теории света X. Гюйгенс вообще игнорировал явление дифракции, а И. Ньютон считал, что дифракция противоречит волновым представлениям о свете и подтверждает корпускулярную точку зрения.

Для объяснения распространения света X. Гюйгенс сформулировал принцип, который назван его именем. Принцип Гюйгенса формулируют так: каждую точку среды, которой достигнет фронт волны в определенный момент времени, можно рассматривать как источник вторичных полусферических волн. Поверхность, огибающая эти элементарные волны, определяет положение фронта волны, которая распространяется в среде, в следующий момент времени. Исходя из принципа Гюйгенса, можно объяснить много явлений, в частности ход лучей при отражении и преломлении света, когда фронт световой волны считается бесконечным, вследствие чего дифракция не возникает. С помощью принципа Гюйгенса можно объяснить захода света в участок геометрической тени, но при этом остается нерешенным вопрос о распределение энергии вдоль волнового фронта. Этот недостаток принципа Гюйгенса было устранено 1815 г. О. Френелем, который дополнил его принципом интерференции вторичных волн. За Френелем, волну, что приходит в любую точку пространства от первичного источника, можно рассматривать как следствие интерференции вторичных волн, приходящих в эту точку от большого количества элементарных вторичных волн определенного волнового фронта. С таким дополнением принцип Гюйгенса называют принципом Гюйгенса - Френеля. По принципу Гюйгенса - Френеля при распространении в пространстве ограниченных фронтов световых волн будет наблюдаться лишь свет там, где элементарные волны, которые излучаются всеми точками фронта волны, распространяется, добавляясь (інтерферуючи), усиливают друг друга. Наоборот, в тех местах, где элементарные волны при наложении гасят друг друга, будет наблюдаться затмение. С помощью принципа Гюйгенса - Френеля можно объяснить все дифракционные явления, а также прямолинейное распространение света. Однако расчеты дифракционных картин связаны с большими математическими труднощами. их можно во многих случаях избежать, если воспользоваться методом зон Френеля. Метод зон Френеля заключается в том, что фронт волны разбивают не на отдельные точечные источники (каждый фронт волны содержит в себе бесконечное количество таких источников), а на определенные участки - зоны. Ширина зон определяется тем, что расстояния от границ соседних зон до точки наблюдения отличаются на половину длины волны. В связи с этим колебания, приходят в точку наблюдения от аналогичных точек соседних зон, а вместе с тем и результирующие колебания от этих зон, будут отличаться по фазе на величину п. Итак, в результате интерференции эти колебания послаблятимуть друг друга.

Применим метод зон Френеля для объяснения явления прямолинейного распространение света в однородной среде. Пусть S₀ - точечный источник (рис. 12.11), М - произвольная точка, в которой надо определить амплитуду Е световых колебаний, S - положение фронта сферической волны в определенный момент времени. Построим зоны Френеля. Границей первой (центральной) зоны Френеля есть точки поверхности S, которые находятся на расстоянии L + λ/2 от точки Г (L - кратчайшее расстояние между точкой М и фронтом волны S). Точки сферы S, лежащие на расстоянии L + 2λ/2, образуют границу второй зоны и т. д. Если амплитуды колебаний, что возмущаются отдельно первой, второй и т. д. зонами, равны соответственно Е₁, Е₂,... ,тo

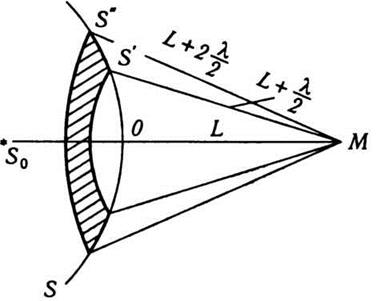
Рис. 12.11

По теории Френеля величина Е_и зависит от площади σ_и соответствующей зоны и α_и - угла между внешней нормалью к поверхности i-й зоны в некоторой ее точке и прямой, проведенной из этой точки в точку М. Математически можно доказать, что построенные зоны Френеля будут одинаковые площади. Однако с увеличением номера зоны увеличивается угол α_и и, согласно гипотезе Френеля, уменьшается интенсивность излучения в направлении точки М, т.е. уменьшается амплитуда Е_и. При α_и = 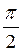Е_i = 0. Следовательно, Е₁ > Е₂ > Е₃ .... При этом можно положить, что

Учитывая (12.17) и уменьшение амплитуды с ростом номера зоны, формулу (12.16) можно переписать так:

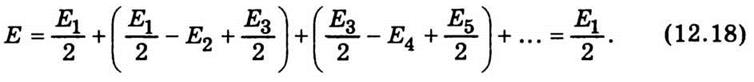
Формула (12.18) показывает, что результирующая действие в точке М полностью открытого фронта световых волн, распространяется от источника S₀, равна половине действия одной центральной зоны. Как показывают математические расчеты, радиус этой зоны сравнительно мал. Так, при S₀O = ОМ = 10 см и λ = 5 ∙ 10^-5 см r ≈ 0,016 см. Следовательно, с большой точностью можно считать, что в свободном пространстве свет от источника S₀ в точку М распространяется прямолинейно.

Дифракционные явления по своему характеру разделяют на два класса. Первый - когда точка наблюдения дифракционной картины размещается на скінченній расстоянии от экрана. Явления этого класса впервые изучил Френель, поэтому их называют дифракцией Френеля. Второй - когда источник света и точка наблюдения дифракционной картины лежат на бесконечности. В этом случае лучи, падающие на препятствие, и лучи, которые идущие в точку наблюдения, практически параллельны. Такую дифракцию впервые изучил И. Фраунгофер, поэтому ее называют дифракцией Фраунгофера.