Часть 4

ОПТИКА. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ

Раздел 12 ВОЛНОВЫЕ СВОЙСТВА СВЕТА

12.2. Интерференция света

Для световых волн сбывается принцип суперпозиции, вследствие чего для них характерно векторное сложение напряженностей электрических полей отдельных световых волн. Справедливость принципа суперпозиции обусловлена тем, что приведены в среде дипольные моменты прямо пропорциональны напряженности внешнего электрического поля, т.е. электрические свойства среды имеют линейный характер. Если бы соотношение между внешним полем и результатом его воздействия на среду имели нелинейный характер, то принципа суперпозиции не было бы. В этом случае одно излучения мешало бы распространению второго, искажало бы его. Однако в некоторых случаях эта нелинейность существует, например при распространении электромагнитных волн в сильно ионизированном среде (плазме). Характерно, что М. В. Ломоносов считал справедливость принципа суперпозиции в области световых явлений одним из основных аргументов в пользу волновой природы света. По электромагнитной теории принцип суперпозиции означает, что вектор напряженности результирующего электрического поля двух световых волн, которые проходят через одну точку, равна векторной сумме напряженностей электрических полей каждой волны отдельно. В частности, если напряженности этих полей имеют одинаковые значение и противоположно направленные, напряженность результирующего электрического поля равна нулю; наоборот, при одинаковом направлении напряженностей составляющих полей напряженность результирующего поля достигнет максимального значения. Явление сложения электромагнитных волн одной частоты колебаний, имеющих постоянную разницу фаз и одинаковое направление колебаний, называют интерференцией электромагнитных волн.

Электромагнитное поле световой волны быстро меняется со временем. Примерно 10¹⁵ раз за секунду напряженность электрического поля проходит через нуль, меняя свое направление, и столько же раз достигает своего максимального значения. Зрительное впечатление обусловлено средним значением квадрата электрического вектора волны за сравнительно большой промежуток времени, а не значением его в каждый момент. Большой промежуток времени, конечно, надо понимать как большой по сравнению с периодом светового колебания, который составляет около 10^-15 с.

Понятно, что глаз увидит усиления или затухания света только тогда, когда этот эффект для многих колебаний, т.е. когда разность фаз между колебаниями інтерферуючими остается постоянной. Следовательно, для возникновения интерференции световых волн в любой точке пространства нужна постоянство разности фаз между одинаково напрямленими световыми колебаниями одинаковой частоты, приходящих в эту точку. Такие колебания называют когерентными.

Любое светящееся тело состоит из очень многих источников колебаний: световые волны порождаются отдельными атомами. вещества. Мы наблюдаем всегда суммарное воздействие многих атомов. Для возникновения интерференции от двух источников света нужно, чтобы в месте наблюдения волны, которые излучаются всеми атомами одного источника, отличались по фазе на постоянный значение от волн второго источника. Такое совпадение практически невозможно, поэтому между лучами двух разных источников света не может возникнуть явление интерференции. Интерференция наблюдается только тогда, когда световые лучи одного источника каким-то образом (отражением, преломлением) были «раздвоенные» и затем снова сводные. Однако даже в этом случае могут возникнуть некогерентні колебания. Источники света, которые излучают когерентные волны, называют когерентными.

Рассмотрим пример сложения двух когерентных волн, которые распространяются от источников S₁ и S₂, которые находятся на расстоянии в₁ и в₂ соответственно от точки наблюдения А (рис. 12.5). Колебания от источников S₁ и S₂ приходят в точку О с некоторой разностью фаз, которая зависит от разности расстояний y₁ и в₂. Разность фаз возникает даже тогда, когда колебания источников происходит в одной фазе. Запишем уравнения колебательных движений, что приходят в точку О,

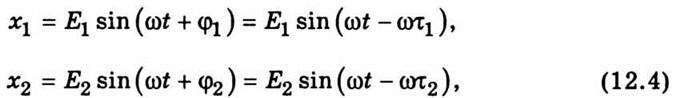
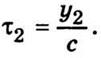где Е₁ и Е₂ - амплитуды колебаний; ω - циклическая частота колебаний; φ₁ и φ₂ - начальные фазы соответствующих колебаний в точке наблюдения; τ₁ и τ₂ - время распространения колебаний от источников S₁ и S₂ до точки наблюдения. Если скорость распространения света c, то и Подставив эти значения в формулу (12.4), получим

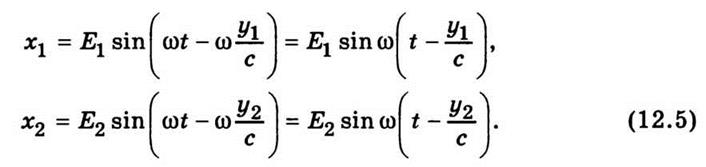
Отсюда следует, что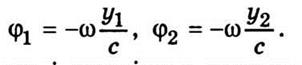

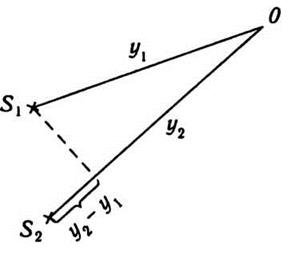
Рис. 12.5

Нас будут интересовать фаза и амплитуда результирующего колебания, попробуем их найти графически. На рис. 12.6 изображены векторную диаграмму сложения двух колебаний с амплитудами соответственно E₁ и Е₂ и начальными фазами φ₁ и φ₂. Из этой диаграммы нетрудно достать формулу для определения фазы результирующего колебания:

Значение амплитуды результирующего колебания достанем из диаграммы как для стороны треугольника, лежащей против тупого угла:

Рис. 12.6

Из формулы (12.7) следует, что амплитуда результирующего колебания определяется не только амплитудами колебаний, что добавляются, но и изменяется в зависимости от разности их начальных фаз. Проанализируем отдельные случаи. Возьмем E₁ = Е₂ = Е₀. Выразим разность фаз через геометрическую разность хода волн:

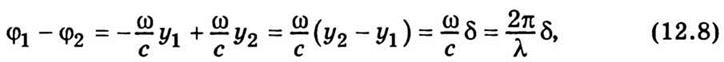
где δ = y₂ - y₁ - геометрическая разность хода волн (см. рис. 12.5); λ - длина волны.

Рассмотрим два предельных случая:

1. Пусть разность фаз кратна 2π: φ₁ - φ₂ = k2π, где k = 0, 2, ... , тогда соs(k2π) = 1. Результирующая амплитуда будет

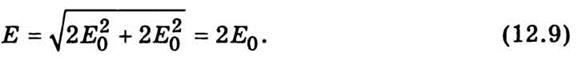
Поскольку интенсивность света пропорциональна квадрату амплитуды электрического вектора, то в этом случае интенсивность результирующего колебания будет в четыре раза больше интенсивности света, которое падает от одного источника. Установим связь между заданной разностью фаз и разностью хода:

Следовательно, интенсивность света в результате интерференции световых лучей увеличивается тогда, когда геометрическая разница хода содержит четное число полуволн.

2. Пусть разность фаз кратна π: φ₁ - φ₂ = (2k + 1)π, тогда соs(2k + 1)π = -1. Результирующая амплитуда будет

Тогда

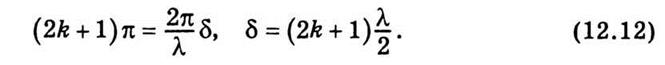
Следовательно, интенсивность света в результате интерференции световых лучей равна нулю, если геометрическая разность хода содержит нечетное число полуволн. Если разность фаз φ₁ - φ₂ хаотически меняется со временем с очень большой частотой порядка 1/t (где t - длительность возбужденного состояния атома), то среднее значение по времени соs(φ₁ - φ₂) будет равна нулю. Результирующая амплитуда двух колебаний при этих условиях будет

Результирующая интенсивность от двух таких источников света при этом равна сумме интенсивностей обоих, которые дает каждое источник. Вследствие того, что наблюдатель не может следить за мгновенным состоянием интерференционной картины, а положение максимумов и минимумов быстро меняется в пространстве, он будет воспринимать некоторую среднюю освещенность без максимумов и минимумов с интенсивностью 2I₀. Источники света, для которых разница фаз хаотически меняется со временем, не могут давать интерференции света с последовательными чередованиями максимумов и минимумов освітленості. их называют некогерентными. Любые независимые источники света, например обычные осветительные лампы, являются некогерентными источниками света: с увеличением их количества интенсивность результирующего освещения никогда не уменьшается. Следовательно, для некогерентних источников света интенсивность результирующего света равна сумме интенсивностей падающего света (I = I₁ + I₂). Для когерентных источников, как было показано выше, такое равенство не выполняется.